Cuando las cargas se aplican a un sólido, éste intenta absorber sus efectos desarrollando fuerzas internas que, en general, varían de un punto a otro. La intensidad de estas fuerzas internas se denomina tensión. Las unidades de tensión son la fuerza por área de unidad
Componentes de la tensión
Pongamos por ejemplo una barra bajo compresión. El estado de los esfuerzos en el punto P se puede describir en términos de un plano arbitrario. Aunque la tensión resultante es la misma en todos los casos, los valores de los componentes de tensión dependen del plano elegido.

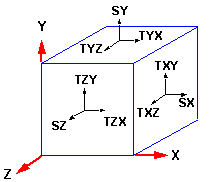
Por tanto, la tensión se describe por magnitud, dirección y el plano en el que actúa. El estado de los esfuerzos en un punto lo describen por completo los siguientes componentes:
|
SX
|
Tensión en la dirección X que actúa con normalidad en el plano YZ.
|
|
SY
|
Tensión en la dirección Y que actúa con normalidad en el plano XZ.
|
|
SZ:
|
Tensión en la dirección Z que actúa con normalidad en el plano XY.
|
|
TXY
|
Tensión en la dirección Y que actúa con normalidad en la dirección X (plano YZ)
|
|
TYX:
|
Tensión en la dirección X que actúa con normalidad en la dirección Y (plano XZ)
|
|
TXZ:
|
Tensión en la dirección Z que actúa con normalidad en la dirección X (plano YZ)
|
|
TZX:
|
Tensión en la dirección X que actúa con normalidad en la dirección Z (plano XY)
|
|
TYZ
|
Tensión en la dirección Z que actúa con normalidad en la dirección Y (plano XZ)
|
|
TZY:
|
Tensión en la dirección Y que actúa con normalidad en la dirección Z (plano XY)
|
SX, SY y SZ se denominan tensiones normales. TXY, ...., TZY se denominan tensiones cortantes. Las tensiones cortantes se relacionan mediante las siguientes ecuaciones: TXY = TYX, TXZ = TZX, and TYZ = TZY. De este modo, el estado de tensión en un punto queda completamente definido por seis componentes.
Tensiones principales
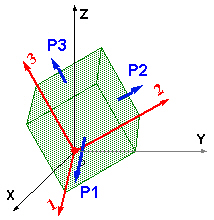
Para cada punto, existe un plano en el cual no hay tensiones cortantes. El estado de tensiones con referencia a este plano queda definido por completo por las tensiones normales, denominadas tensiones principales.
|
P1
|
Tensión normal en la primera dirección principal (más grande).
|
|
P2
|
Tensión normal en la segunda dirección principal (intermedia).
|
|
P3
|
Tensión normal en la tercera dirección principal (más pequeña).
|
|
|
Tensión equivalente (también denominada tensión de von Mises)
En SimulationXpress, puede ver una cantidad de tensión denominada tensión equivalente (o de von Mises). Mientras que una tensión equivalente en un punto no define exclusivamente el estado de tensión en él, proporciona información adecuada para evaluar la seguridad del diseño para múltiples materiales dúctiles.
A diferencia de los componentes de tensión, la tensión equivalente no tiene dirección. Está completamente definida por la magnitud con unidades de tensión. Para calcular los factores de seguridad en diferentes puntos, SimulationXpress utiliza el Criterio de flexibilidad de von Mises, según el cual un material empieza a ser flexible en un punto cuando la tensión equivalente alcanza el límite elástico del material.