불규칙 진동 환경에서 작동하는 부품에 대한 피로 손상 평가는 반응 응력 PSD(파워 스펙트럼 밀도) 함수의 통계 속성을 기반으로 하는 진동수 영역에서 진행됩니다.
구조 또는 기계 부품이 바람 하중을 받는 풍력 터빈, 파도 하중을 받는 해양 구조물 또는 다양한 도로 표면 프로파일에서 작동하는 자동차 엔진과 같이 불규칙 하중 형식일 경우 피로 수명은 진동수 영역에서 평가됩니다.
기간 진동 피로(또는 진동수 기반 피로)는 부하 및 응답(응력 및 변형 내역)이 불규칙한 피로 수명의 평가를 참조하기 때문에 파워 스펙트럼 밀도(PSD 함수)와 같은 통계 수치를 사용할 때 가장 잘 나타낼 수 있습니다.
응답 응력 PSD의 통계 특성은 PSD 함수의 모멘트를 통해 얻을 수 있습니다.
| PSD의 통계 특성 |
수식 |
|---|
| 진동수 f(Hz 단위)에서 응력 PSD S(f)의 n번째스펙트럼 모멘트입니다. |
 (수식 1) (수식 1)
|
| 연속적인 고정 가우스 과정 σ에 대한 RMS(평균 평방근) 값입니다. |
 수식 2) 수식 2)
|
| 일반적인 1초 샘플에 대한 상승하는 영점 교차 E[0]의 평균 개수입니다. |
 (수식 3) (수식 3)
|
| 일반적인 1초 샘플에 대한 최고점 E[p]의 평균 개수입니다. |
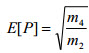 (수식 4) (수식 4)
|
| 불규칙성 계수 γ는 0과 1 사이에서 결정됩니다. 응력 신호가 협대역 과정에 접근하면 1에 접근합니다(사인파 γ =1의 경우). 응력 신호가 화이트 노이즈 과정에 접근하면 0에 접근합니다 |
 (수식 5) (수식 5)
또는
 (수식 6) (수식 6)
|
재질 피로 속성은 보통 S-N 곡선에서 얻는데, 이 곡선은 응력 범위 S(장력의 최대 반복 응력과 압축의 최소 반복 응력 사이의 응력 편차)와 평균 실패 싸이클 N 사이의 관계를 정의합니다.
가장 높은 싸이클 피로 문제(N >= 104 )의 경우 S-N 곡선을 간단한 식으로 나타낼 수 있습니다.
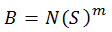 (수식 7)
(수식 7)
B와 m은 부하와 환경 조건이 다른 재질 속성이며 피로 테스트 실험으로 결정됩니다.
불규칙 하중의 피로로 인해 축적된 손상 E[AD]는 팔므그렌 마이너 법칙을 기반으로 하며 다음과 같이 나타냅니다.
 (수식 8)
(수식 8)
n(S)는 응력 범위 레벨 S에 적용된 싸이클 개수이고 p(S)는 응력 범위의 확률 밀도 함수입니다. 위 방정식에서 간단한 S-N 곡선 방정식을 대체하면 다음과 같은 불규칙 응력 응답의 일반적인 피로 손상 방정식이 얻어집니다.
 (수식 9)에서 T는 불규칙 부하의 지속 시간(초 단위)입니다.
(수식 9)에서 T는 불규칙 부하의 지속 시간(초 단위)입니다.
수식 9를 기반으로 하는 피로 손상 평가 방법으로는, Steinberg의 Three Band 방법, Narrow Band 방법 및 Wirshing 방법과 같이 세 가지 종류가 있습니다. 각 방법은 다양한 확률 밀도 함수 p(S) 정의를 사용합니다.
Narrow Band 방법
Narrow Band 방법에서 협대역 신호의 최고점에 대한 확률 밀도 함수는 Rayleigh 분포를 나타내는 경향이 있습니다(Bendat J.S., Probability Functions for Random Responses. Contact NASA-5-4590에 대한 NASA 보고서, 1964).
 (수식 10)
(수식 10)
(수식 10)을 (수식 9)로 대체하고 결과를 피로 손상 평가에 대한 다음 식으로 통합합니다.
 (수식 11)에서 Γ(.)는 감마 함수입니다.
(수식 11)에서 Γ(.)는 감마 함수입니다.
Wirsching 방법
Wirsching 방법(Wirshing, P.H., Paez, T.L. 및 Ortiz K., Random Vibration, John Wiley & Sons Inc., New York, 1995)은 Narrow Band 방법을 실험 수정 계수로 수정하여 광대역 과정을 고려합니다.
 (수식 12
(수식 12
 (수식 13
(수식 13
ζw 는 다양한 스펙트럼 밀도 함수를 포함하는 몬테 카를로 시뮬레이션에서 파생된 실험 계수입니다.
αw 및 bw는 다음에서 제공된 최적의 파라미터입니다.
 (수식 14
(수식 14
Steinberg의 Three Band 방법
Steinberg 방법에서는 불규칙 응력 응답의 확률 밀도 함수는 가우스 분포를 따르기 때문에 응력 응답 진폭의 예상값은 다음과 같이 특정 확률 레벨에 따라 다르다고 가정합니다.
- 응력 싸이클의 진폭이 응력 응답 신호의 평균 평방근 2배 범위를 초과하지 않을 가능성은 68.27%입니다.
- 응력 싸이클의 진폭이 응력 응답 신호의 평균 평방근 4배 범위를 초과하지 않을 가능성은 27.1%입니다.
- 응력 싸이클이 응력 응답 신호의 평균 평방근 6배 범위를 초과하지 않을 가능성은 4.3%입니다.
범위가 평균 평방근의 6배를 초과하는 응력 싸이클은 없습니다.
예상 피로 손상은 다음 방정식으로 구해집니다.
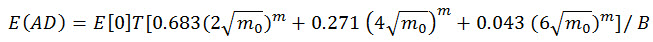 (수식 15)
(수식 15)
시뮬레이션에서 응력 PSD 함수는 피로 해석 스터디가 기반으로 하는 동적-불규칙 진동 스터디 결과입니다. 3가지 방법 모두에서 피로로 인한 예상 손상 계산에는 vonMises 응력 부품이 고려됩니다.