Analysis Procedure - Harmonic

Harmonic analysis evaluates peak steady state response of a system to harmonic loads.

At each solution step, all applied loads and base excitations have the same frequency. The magnitudes are defined by the associated frequency curves.

Assume a harmonic nodal force vector {P} defined as:

(Equation 1) or (Equation 2),

where:

P_k is the magnitude of the force in the direction of the k^th degree of freedom

ω is the exciting frequency, and

γ_k is the phase angle of the force.

For linear systems, the system's equations of motion are de-coupled into n modal equations:

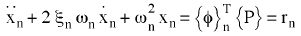(Equation 3).

Substituting the force vector {P} into (Equation 3) results in:

(Equation 4), where

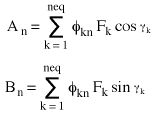(Equation 5)

The steady state solution to (Equation 4) is:

(Equation 6).

The real part of (Equation 6) is:

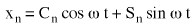(Equation 7) where

(Equation 8) and

(Equation 9).

The displacement vector u is given by:

(Equation 10) or

(Equation 11)

The magnitude of the displacement u_k and the corresponding phase angle θ_kfor the k^th degree of freedom are:

(Equation 12)

The velocity and acceleration responses are derived from the derivatives of (Equation 11). Their amplitudes are:

(Equation 13)

The velocities and accelerations phase angles are 90º and 180º out of phase with respect to the displacement phase angles.