El sistema de ecuaciones de movimiento para un sistema n grados de libertad excitado por una fuerza dependiente del tiempo es el siguiente:
(Ecuación 1)
Mediante la utilización de una transformación de coordenadas, el conjunto de n ecuaciones simultáneas se reduce a n ecuaciones independientes (cada ecuación se soluciona por separado):
para r = 1, 2, ...., n (Ecuación 2)
donde xr(t) son las coordenadas modales relacionadas con las nodales ur(t) mediante:
(Ecuación 3).
El vector de las cargas modales {m(t)} viene dado por:
(Ecuación 4).
Si suponemos que las excitaciones se expresan por sus funciones de densidad espectral de potencia (psd), la solución puede formularse en el dominio de frecuencia. Si la matriz psd de excitación es [Sf(ω)], la matriz psd de fuerza modal se define como:
(Ecuación 5).
La psd de la respuesta de desplazamiento modal [Sx(ω)] se obtiene a partir de:
(Ecuación 6),
donde [H(ω)] es la matriz de función de transferencia modal y [H*(ω)] es su conjugación compleja. Para modos normales, la matriz de función de transferencia es diagonal con elementos diagonales Hr(ω)
(Ecuación 7) y
(Ecuación 8).
La psd de la respuesta de desplazamiento [Su(ω)] se deriva, por tanto, de (Ecuación 3).
(Ecuación 9).
La psd de las respuestas de velocidad y aceleración se expresa como:
(Ecuación 10) y
(Ecuación 11).
La velocidad modal y psd de la aceleración están relacionadas con la psd del desplazamiento modal a través de:
(Ecuación 12) y 
(Ecuación 13)
Ecuación 10 y Ecuación 11 pueden volver a formularse como:
(Ecuación 14) y 
(Ecuación 15).
Las respuestas de autocorrelación modal de retraso nulo (τ=0) en términos de psd de respuesta modal se calculan a partir de sus integrales:
(Ecuación 16)
(Ecuación 17)
(Ecuación 18).
A partir de las ecuaciones anteriores, las respuestas de media cuadrática se determinan a partir de los términos diagonales de las matrices:
(Ecuación 19),
(Ecuación 20),
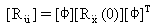(Ecuación 21).
Respuesta de media cuadrática de la tensión
Los elementos de tensión {σ} se calculan a partir de los desplazamientos nodales {u} así:
(Ecuación 22) o en términos de desplazamientos modales {x}:
(Ecuación 23), donde [Φ] es la matriz de autovectores.
La matriz de correlación de tensión [Rσ] viene dada por:
(Ecuación 24).