應力週期的其他替換應力振幅計算方式為此週期的應力範圍之一半。應力週期造成的損害量不只根據其他替換應力,也會視平均應力而定。例如,以下兩個週期具有相同的其他替換應力,但由於其平均應力不同,所以造成的損害量也不同。

下圖 (稱為 Haigh 圖) 表示平均應力對發生失敗的週期數之影響。
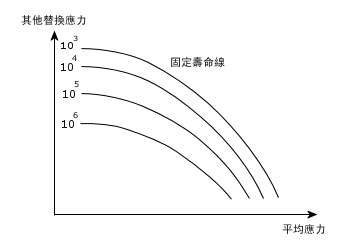
只有當負載為完全反覆時,平均應力才會為零。最明顯的例子就是 R 比例與提供的負載相同之 S-N 曲線。在此狀況中,會直接使用 S-N 曲線,因為不需任何修正。如果您定義了具有不同 R 比例的 S-N 曲線,軟體就會以線性內插法來計算曲線之間的平均應力。只有當 S-N 曲線的 R 比例與提供的負載之 R 比例不同時才需要修正。
程式一律使用 von Mises 應力來計算平均應力。 由於 von Mises 為正值,程式會指定具有最大代數值的主應力正負值,以計算相關的平均應力。
定義
為討論修正方式,我們為一應力週期定義下列變數:
Smax = 最大應力
Smin = 最小應力
ΔS = 應力範圍 = Smax - Smin
Sa = 其他替換應力 = (Smax - Smin)/2
Smean = 平均應力 = (Smax + Smin)/2
R = 應力比例 = Smin/Smax
A = 振幅比例 = Sa/Smean
以下列出一些共用負載的應力及振幅比例:
| 負載類型
|
應力及振幅比例
|
|---|
| 完全反覆
|
R = -1,A = 無限值
|
| 零到最大
|
R = 0,A = 1
|
| 零到最小
|
R = 無限值,A = -1
|
修正方法
以下假設:
Sca = 修正的其他替換應力(根據零平均),
Sy = 降伏強度,以及
Su = 最大強度
本軟體提供下列方法來計算 S
ca:
| 方法
|
數學關係式
|
|---|
| 1. Goodman 方法 - 通常適合易碎的材料:
|

|
| 2. Gerber 方法 - 通常適合可延展的材料
|
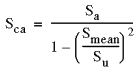
|
| 3. Soderberg 方法 - 通常是最保守的方法
|
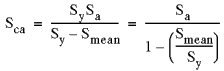
|
對於變化及固定振幅事件,除了每個週期的其他替換應力之外,軟體還會計算平均應力,然後使用指定的準則來估計修正的應力。