Sistemi con grado di libertà singolo (SDOF)
Considerare il sistema semplice di massa-molla. La massa (m) è soggetta ad una forza F(t) nella direzione u come funzione del tempo. La massa è consentita per spostarsi solo nella direzione u e quindi si tratta di un sistema con grado di libertà singolo (SDOF). Il movimento ha come resistenza una molla di rigidezza (k)
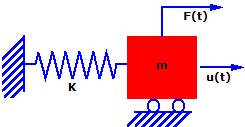
La seconda legge di Newton (forza uguale massa per accelerazione) per questo sistema nel tempo (t) genera:
F(t)-ku(t) = mu..(t)
o:
mu..(t) + ku(t) = F(t)
dove:
u..(t) è l'accelerazione della massa nel tempo (t) ed è uguale alla seconda derivativa di u rispetto al tempo
k = è la rigidità della molla
In teoria, se la massa viene spostata e rilasciata, continuerà a vibrare con la stessa ampiezza per sempre. In pratica, la massa vibra con ampiezze progressivamente più piccole fino a fermarsi. Questo fenomeno è chiamato smorzamento ed è causato dalla perdita di energia attraverso l'attrito e altri effetti. Lo smorzamento è un fenomeno complesso. Per lo scopo di questa discussione, consideriamo che la forza di smorzamento sia proporzionale alla velocità. Questo tipo di smorzamento è chiamato smorzamento viscoso.
Considerando lo smorzamento, l'equazione diventa:
mu..(t) + cu.(t) + ku(t) = F(t)
dove:
u.(t) è la velocità della massa nel tempo (t) ed è uguale alla prima derivativa di u rispetto al tempo
Negli studi statici, la velocità e l'accelerazione sono così piccole che possono essere ignorate ed F e u non sono funzioni del tempo. L'equazione si riduce quindi a: F=ku.
Sistemi con grado di libertà multiplo (MDOF)
Per un sistema con grado di libertà multiplo (MDOF), m, c e k diventano matrici invece di valori singoli e le equazioni del movimento sono espresse in questo modo:
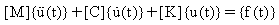
dove:
[M]: matrice di massa
[K] : matrice di rigidezza
[C] : matrice di smorzamento
{u(t)}: vettore di spostamento nel tempo t (componenti di spostamento ad ogni nodo)
: vettore di accelerazione nel tempo t (componenti di accelerazione ad ogni nodo)
: vettore di velocità nel tempo t (componenti di velocità ad ogni nodo)
{f(t)}: vettore con carico che varia nel tempo (componenti di forza ad ogni nodo)