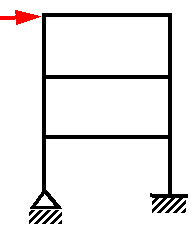
Balkenelemente können Biege-, Schub- und Torsionslasten widerstehen. Der nachstehend gezeigte typische Rahmen ist mit Stäben erstellt, damit die Last an die Stützelemente übertragen wird. Die Modellierung solcher Rahmen mit Stabelementen schlägt fehl, das es keinen Mechanismus zur Übertragung der angewendeten horizontalen Last auf die Stützen gibt.
Bei Balkenelementen muss der genaue Querschnitt definiert werden, damit das Programm die Trägheitsmomente sowie die neutralen Achsen und den Abstand zwischen obersten/untersten Fasern und den neutralen Achsen berechnen kann. Die Spannungen innerhalb der Ebene des Querschnitts und entlang des Balkens sind unterschiedlich.
Denken Sie an einen 3D-Balken mit der Querschnittsfläche (A) und dem dazugehörigen Netz. Balkenelemente können auf der eigentlichen Balkengeometrie oder unabhängig von ihrer tatsächlichen Querschnittsform als hohle Zylinder angezeigt werden.
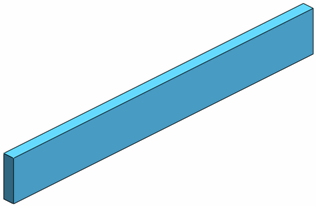
|
| 3D-Geometrie
|

|
| Netz auf Zylindern (jeder hohle Zylinder ist ein Element)
|
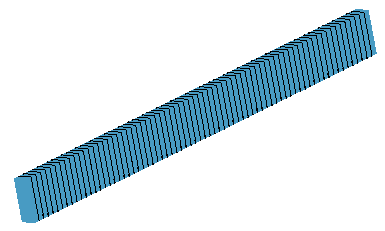
|
| Netz auf Balkengeometrie
|
Die nachstehende Abbildung zeigt ein kleines Balkensegment, das vereinfachten 2D-Kräften (Axialkraft P, Schubkraft V und Biegemoment M) ausgesetzt ist:
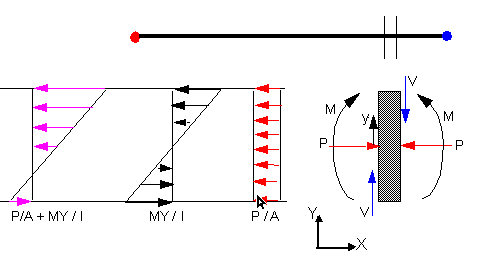
Im Allgemeinen wirken 3 Kräfte und 3 Momente auf das Segment ein.
Gleichmäßige Axialspannung = P/A (ähnlich wie bei Stabelementen)
Gleichmäßige Schubspannung = V/A
Das Biegemoment M verursacht eine Biegespannung, die mit dem vertikalem Abstand y zur neutralen Achse linear variiert.
Biegespannung (biegend in y-Richtung) = My/I
Dabei ist l das Trägheitsmoment bezogen auf die neutrale Achse.
Die Biegespannung ist an den obersten bzw. untersten Fasern am größten. In diesem Beispiel entsteht die größte Druckbelastung an der obersten Faser und die größte Spannung an den untersten Fasern.
Verbindungen
Verbindungen befinden sich an den freien Enden von Strukturbauteilen und am Schnittpunkt von zwei oder mehr Strukturbauteilen. Der PropertyManager für Verbindung bearbeiten enthält ein Werkzeug zur genauen Definition von Verbindungen. Das Programm erstellt in der Querschnittsmitte der einzelnen Bauteile jeweils einen Knoten. Durch Trimmen und Verwendung von verschiedenen Querschnitten für unterschiedliche Bauteile fallen die Knoten der mit einer Verbindungsstelle verbundenen Bauteile u.U. nicht zusammen. Das Programm erstellt spezielle Elemente nahe der Verbindung, um eine starre Verbindung basierend auf geometrischen und materiellen Eigenschaften zu simulieren.
Materialeigenschaften
Elastizitätsmodul und Poissonsche Zahl sind erforderlich.
Dichte ist nur dann notwendig, wenn es sich um Schwerkraftlasten handelt.
Lager
Lager können nur auf Verbindungen angewendet werden. Jede Verbindungsstelle ist mit 6 Freiheitsgraden versehen. Es können Null-Translationen und/oder -Drehungen oder auch vorgeschriebene Translationen und Drehungen ungleich Null angewendet werden.
Verbinden
In einer Studie mit Balken, Volumenkörpern und Schalenflächen können Sie Balken und Balkenverbindungen an Volumenkörper und Schalenflächen binden.
Der Bindungskontakt zwischen angrenzenden Strukturbauteilen mit einer Oberfläche oder Blechfläche wird automatisch erstellt.
Balkenversteifungen für gekrümmte Oberflächen
Sie können (gerade oder gekrümmte) Balken verbinden, die als Versteifungen für gekrümmte Oberflächen von Schalen oder Blechkörpern dienen.
Balken werden automatisch mit gekrümmten Oberflächen verbunden, die sich berührende Geometrien aufweisen oder sich innerhalb eines geeigneten Abstands befinden. Das Programm verwendet Balkenelementgrößen, die kompatibel mit den Oberflächennetzgrößen sind. Das Feature ist für statische Studien sowie für Knick- und Frequenzstudien verfügbar.
Lasten
Sie können Folgendes anwenden:
- Konzentrierte Kräfte und Momente an Verbindungen und Referenzpunkten Für dynamische Studien können Sie zeit- oder frequenzabhängige Lasten anwenden.
- Verteilte Lasten entlang der Gesamtlänge eines Balkens
- Schwerkraftlasten. Das Programm berechnet die Schwerkraft auf Basis der angegebenen Beschleunigungen und Dichten.
- Gleichförmige oder ausgewählte Basiserregung für dynamische Studien.
- Anfangsbedingungen für dynamische Studien. Wenden Sie eine Anfangsverschiebung, Geschwindigkeit oder Beschleunigung (Zeit t=0) an Verbindungen oder Balkensegmenten an.
Vernetzung
Ein Strukturbauteil wird automatisch als Balken identifiziert und mit Balkenelementen vernetzt. Nachdem Sie das Netz erstellt haben, können Sie Vernetzungssteuerungen anwenden, um eine andere Anzahl von Elementen oder eine Elementgröße für ausgewählte Balken anzugeben.
Bauteile aus Balken und Stäben können auf der eigentlichen Balkengeometrie oder unabhängig von ihrer tatsächlichen Querschnittsform als hohle Zylinder angezeigt werden.
Ergebnisse
Die Ergebnisse für die einzelnen Elemente werden in den entsprechenden lokalen Richtungen dargestellt. Es können die gleichmäßigen Axialspannungen, Torsions-, Biege- und Schubspannungen in zwei orthogonalen Richtungen (Richt.1 und Richt.2) sowie die durch Kombination von Axial- und Biegespannungen erzeugte Maximalspannungen an den obersten bzw. untersten Fasern angezeigt werden.
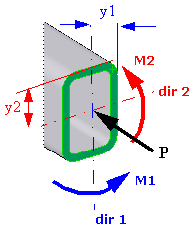
Wie nachstehend gezeigt, ist ein Balken der Axialkraft P und den Momenten M1 und M2 ausgesetzt. Das Moment M1 befindet sich um die Richtung-1-Achse und das Moment M2 befindet sich um die Richtung-2-Achse.
Wenn Sie die Option Balkenprofil rendern (PropertyManager Spannungsdarstellung) auswählen, berechnet die Software Spannungen, die innerhalb der Querschnittsebene variieren. Spannungen werden an beiden Enden jedes Netzelements sowie an Punkten des Querschnitts mit unterschiedlicher Entfernung von der neutralen Achse des Balkens berechnet.
Wenn die Option Balkenprofil rendern deaktiviert ist, berechnet die Software die Spannungswerte an den obersten bzw. untersten Fasern jedes Balkenendes. Sie meldet den größten Spannungswert für jedes Balkensegment.
| Axial |
Gleichmäßige Axialspannung = P/A
|
| Obere Biegung in RICHT 1 |
Größter Wert der Biegespannung aufgrund von Moment M1 (Biegen Ms/Ss im Darstellungsnamen, Titel und in der Legende). |
| Obere Biegung in RICHT 2 |
Größter Wert der Biegespannung aufgrund von Moment M2 (Biegen Mt/St im Darstellungsnamen, Titel und in der Legende). |
| Obere Axial- und Biegespannung |
Die Software berechnet die höchsten Spannungen an den obersten bzw. untersten Fasern des Querschnitts, indem die gleichmäßige Axialspannung und die beiden Biegespannungen aufgrund von M1 und M2 kombiniert werden. Dies ist die empfohlene Spannungsanzeige. Die Spannungswerte werden an beiden Enden jedes Netzelements berechnet:
P/ A + [(M1* I22 + M2 * I12) * y1 + ( M2 * I11 + M1 * I21) * y2)] / (I22 * I11 - I12^2)
wobei I ij (i = j = 1 oder 2) die Trägheitsmomente an den jeweiligen lokalen orthogonalen Balkenrichtungen 1 und 2 sind.
|