Die Wechselspannungsamplitude für einen Spannungszyklus ergibt sich aus der Hälfte des Spannungsbereichs im Zyklus. Der durch einen Spannungszyklus verursachte Schadensumfang hängt nicht nur von der Wechselspannung, sondern auch von der Mittelspannung ab. Zum Beispiel haben die beiden unten dargestellten Zyklen dieselbe Wechselspannung. Da sie aber unterschiedliche Mittelspannungswerte aufweisen, verursachen sie verschiedene Schadensbeträge.

Die Auswirkung von Mittelspannungen auf die Anzahl der Zyklen bis zum Versagen wird durch das folgende Diagramm, das so genannte Haigh-Diagramm, veranschaulicht.
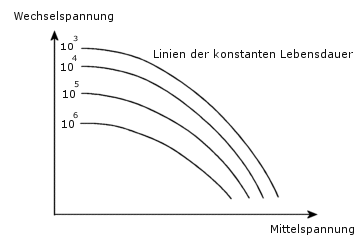
Die Mittelspannung ist nur dann Null, wenn die Last vollkommen reversibel ist. Der einfachste Fall liegt vor, wenn eine Wöhlerkurve mit demselben R-Verhältnis wie bei der Belastung verfügbar ist. In diesem Fall wird die Wöhlerkurve direkt verwendet, da keine Korrektur erforderlich ist. Wenn Sie Wöhlerkurven mit unterschiedlichen R-Verhältnissen definieren, berücksichtigt die Software die Mittelspannung durch lineare Interpolation zwischen den Kurven. Wenn nur eine Wöhlerkurve mit einem R-Verhältnis verfügbar ist, das sich vom R-Verhältnis der Belastung unterscheidet, wird eine Korrektur benötigt.
Das Programm verwendet immer die von-Mises-Spannung zum Berechnen der Mittelspannung. Da die von-Mises-Spannung eine positive Größe ist, wird dieser Spannung das Vorzeichen der Hauptspannung mit der größten algebraischen Magnitude zugewiesen, um die zugehörige Mittelspannung zu berechnen.
Definitionen
Um die Korrekturmethoden zu erläutern, werden die folgenden Variablen für einen Spannungszyklus definiert:
Smax = Maximale Spannung
Smin = Minimale Spannung
ΔS = Spannungsbereich = Smax - Smin
Sa = Wechselspannung = (Smax - Smin)/2
Smean = Mittelspannung = (Smax +Smin)/2
R = Spannungsverhältnis = Smin/Smean
A = Amplitudenverhältnis = Sa/Smean
Im Folgenden sind die Spannungs- und Amplitudenverhältnisse für einige häufig verwendete Lasten aufgeführt:
| Lastart
|
Spannungs- und Amplitudenverhältnisse
|
|---|
| Vollständig umgekehrt
|
R = -1, A = unendlich
|
| Null bis Maximum
|
R = 0, A = 1
|
| Null bis Minimum
|
R = unendlich, A = -1
|
Korrekturmethoden
Die folgenden Abkürzungen haben die folgende Bedeutung:
Sca = Korrigierte Wechselspannung (basierend auf Mittelwert 0)
Sy = Fließspannung
Su = Bruchgrenze
Die Software bietet die folgenden Methoden zum Berechnen von S
ca:
| Methode
|
Gleichung
|
|---|
| 1. Goodman-Methode – im Allgemeinen für spröde Materialien geeignet
|

|
| 2. Gerber-Methode – im Allgemeinen für dehnbare Materialien geeignet
|

|
| 3. Soderberg-Methode – im Allgemeinen die konservativste Methode
|

|
Bei Ereignissen mit variabler oder konstanter Amplitude berechnet die Software die Mittelspannung zusätzlich zur Wechselspannung für jeden Zyklus und berechnet dann die korrigierte Spannung mit den angegebenen Kriterien.