Die Fließkriterien können wie folgt definiert werden: 
Dabei ist
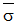
die Wirkspannung und σ
Y die Fließspannung aus uniaxialen Tests. Das von-Mises-Modell kann zum Beschreiben des Verhaltens von Metallen verwendet werden. Bei der Verwendung dieses Materialmodells müssen folgende Überlegungen beachtet werden:
-
Verformbarkeit bei geringer Dehnung wird angenommen, wenn kleine oder große Verschiebungen verwendet werden.
- Es wird eine zugehörige Fließregelannahme getroffen.
- Sowohl isotrope als auch kinematische Erhärtungsregeln sind verfügbar. Eine lineare Kombination isotroper und kinematischer Erhärtung wird implementiert, wenn der Radius und die Mitte der Streckoberfläche in abweichendem Raum hinsichtlich der Belastungshistorie variieren können.
Der Parameter RK definiert die Proportion kinematischer und isotroper Erhärtung. Für rein isotrope Erhärtung hat der Parameter RK den Wert 0. Der Radius der Streckoberfläche nimmt zu aber die Mitte bleibt im abweichenden Raum fixiert. Für rein kinematische Erhärtung hat der Parameter RK den Wert 1. Der Radius der Streckoberfläche bleibt konstant, während die Mitte im abweichenden Raum beweglich ist.
Eine bilineare oder multilineare uniaxiale Spannungs-Dehnungskurve für Verformbarkeit kann eingegeben werden. Für die bilineare Spannungs-Dehnungskurven-Definition werden die Fließgrenze, das Elastizitätsmodul und das Tangentialmodul mithilfe des Dialogfelds Material eingegeben. Für die multilineare Spannungs-Dehnungskurven-Definition sollte eine Spannungs-Dehnungskurve definiert werden.

Wenn Sie eine Spannungs-Dehnungs-Kurve definieren, sollte der erste Punkt auf der Kurve der Fließpunkt des Materials sein. Materialeigenschaften wie Elastizitätsmodul, Fließgrenze usw. werden der Spannungs-Dehnungskurve entnommen, wenn sie verfügbar ist, und nicht der Tabelle mit den Materialeigenschaften im Dialogfeld Material. Lediglich die Poissonsche Zahl (NUXY) stammt aus dieser Tabelle.
Fallprüfungsstudien können nur bilineare Spannungs-Dehnungskurven für Plastizität verwenden. Wenn Sie eine multilineare Spannungs-Dehnungskurve definieren und eine Fallprüfungsstudie ausführen, wird sie vom Solver ignoriert.
Die Parameter Fließspannung und Elastizitätsmodul für die Beschreibung der bilinearen Spannungs-Dehnungskurve können mit Temperaturkurven verbunden werden, um die thermoplastische Analyse durchzuführen. Thermoplastizität ist für Schalenelemente nicht verfügbar.
Das Huber-von Mises-Modell kann mit Volumenkörperelementen (Entwurf und hohe Qualität) und dickwandigen Schalenelementen (Entwurf und hohe Qualität) verwendet werden.
Der Einsatz der iterativen NR (Newton-Raphson)-Methode wird empfohlen.
Typische Spannungs-Dehnungskurve eines Kunststoffs:
