Nella teoria della plasticità con forte deformazione, viene definito il valore della deformazione logaritmica come: 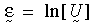
dove U è il tensore di stiramento destro solitamente ottenuto dalla scomposizione del polo destro del gradiente di deformazione F (ad esempio, F = R U, R è il tensore di rotazione). La deformazione logaritmica incrementale è calcolata come: 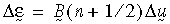
dove B(n+1/2) è la matrice di deformazione-spostamento stimata al passo di soluzione n+1/2 e Δu è il vettore degli spostamenti incrementali. Si osservi che la formula sopra riportata è un'approssimazione di secondo ordine della formula esatta.
Il coefficiente di sollecitazione è preso dal coefficiente Green-Naghdi per garantire la correttezza del modello costitutivo. Trasformando il coefficiente di sollecitazione dal sistema globale al sistema R:
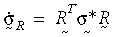
L'intero modello costitutivo avrà la stessa forma della teoria della lieve deformazione. La teoria della plasticità da forte deformazione viene applicata al criterio di snervamento von Mises, alla regola di flusso associativo e all'indurimento cinematico e isotropo (bilineare o multilineare). La dipendenza dalla temperatura della proprietà del materiale è supportata dall'indurimento bilineare. Nel presente caso, viene usato l'algoritmo di ritorno radiale. L'idea di base è approssimare il vettore normale N con:
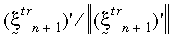
dove 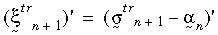
Nella seguente figura vengono illustrate le due precedenti equazioni.
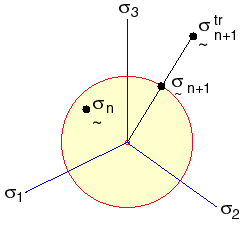
Il vettore di forza dell'elemento e le matrici di rigidezza sono calcolati in base alla formula di Lagrange aggiornata. Le sollecitazioni di Cauchy, le deformazioni logaritmiche e lo spessore attuale (solo elementi shell) sono salvati nel file di output.
L'elasticità nel presente caso è modellata in forma iperelastica, presupponendo piccole deformazioni elastiche e consentendo arbitrariamente forti deformazioni plastiche. Per i problemi di elasticità di forte deformazione (materiali gommosi), è possibile utilizzare modelli di materiali iperelastici, come ad esempio Mooney-Rivlin.
la sollecitazione Cauchy (vera) e la deformazione logaritmica devono essere utilizzate nella definizione della curva di sollecitazione-deformazione multi-lineare.