Le forze interne di un corpo variano da un punto a un altro. In una qualsiasi area piccola del piano interno, una parte del corpo su un lato dell'area applica i carichi alla parte sull'altro lato. La sollecitazione denota l'intensità di queste forze interne (forza per unità di area).
Sollecitazione
In un corpo continuo, è possibile calcolare la sollecitazione di un punto:
- Si immagini un piano arbitrario che taglia il corpo in tale punto,
- Considerare un'area microscopica ΔA intorno a quel punto sul piano,
- Supponiamo che il modulo della forza trasmessa attraverso ΔA in una certa direzione sia ΔF,
- La sollecitazione in tale direzione viene data da ΔF/ΔA quando ΔA si avvicina a 0.
quanto sopra definisce una sollecitazione o un vettore di trazione su un punto. Il vettore di trazione non definisce unicamente lo stato di sollecitazione su un punto. Esso varia secondo il piano arbitrario scelto. Un tensore di sollecitazione, ad esempio un vero tensore di sollecitazione definito come σ = n.T (moltiplicazione matrice), dove n è il vettore normale associato al piano e T è lo stress o il vettore di trazione, definisce univocamente la sollecitazione.
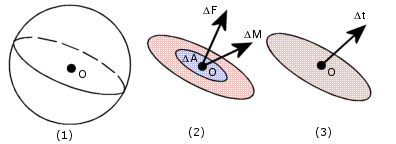
Figura (1): un piano che passa per un punto O e divide il corpo in due parti.
Figura (2): La forza che ne risulta ed i vettori momento su una regione dell'area ΔA relativa al punto O nel piano.
Figura (3): vettore di sollecitazione limite nel punto O nel piano.
Deformazione
La deformazione è il rapporto della variazione in lunghezza δL rispetto alla lunghezza L originale. La deformazione è una grandezza senza dimensione.
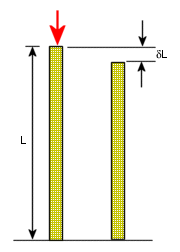
Deformazione = δL/L
Sequenza dei calcoli
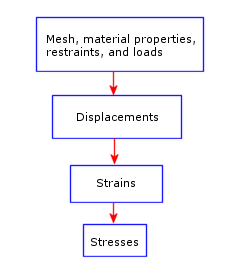
Dato un modello con mesh con un gruppo di vincoli e carichi di spostamento, il software di analisi statica lineare procederà nel modo seguente:
- Il software costruisce e risolve un sistema simultaneo di equazioni di equilibrio degli elementi finiti lineari per calcolare i componenti di spostamento ad ogni nodo.
- Il software quindi usa i risultati di spostamento per calcolare i componenti di deformazione.
- Il programma utilizza i risultati di deformazione e le relazioni deformazione-sollecitazione per calcolare le sollecitazioni.
Calcoli della sollecitazione
I risultati della sollecitazione vengono per prima cosa calcolati in punti speciali, chiamati punti gaussiani o punti di quadratura, posizionati all'interno di ciascun elemento. Questi punti sono selezionati per fornire risultati numerici ottimali. Il programma calcola le sollecitazioni di ciascun elemento estrapolando i risultati disponibili nei punti gaussiani.
Dopo un'iterazione positiva della soluzione, i risultati della sollecitazione nodale in ogni nodo di ciascun elemento sono disponibili nel database. I nodi comuni a uno o più elementi hanno risultati multipli. In generale, questi risultati non sono identici perché il metodo degli elementi finiti è un metodo approssimativo. Ad esempio, se un nodo è comune a tre elementi, possono esistere tre valori leggermente diversi per ogni componente di sollecitazione in tale nodo.
Quando si visualizzano i risultati della sollecitazione, è possibile richiedere le sollecitazioni dell'elemento o quelle nodali. Per calcolare le sollecitazioni dell'elemento, il programma esegue la media delle sollecitazioni nodali corrispondenti per ogni elemento. Per calcolare le sollecitazioni nodali, il programma esegue la media dei risultati corrispondenti da tutti gli elementi che condividono il nodo.