Harmonik analiz, bir sistemin harmonik yüklere verdiği tepe kararlı hal yanıtını değerlendirir.
Her çözüm adımında, uygulanan tüm yükler ve taban uyarımları aynı frekansa sahiptir. Genlikler, ilişkili frekans eğrileri tarafından tanımlanır.
Bir harmonik düğüm kuvveti vektörünün {P} şu şekilde tanımlandığını varsayın:
(Denklem 1) veya 
(Denklem 2),
Burada;
Pk, kth serbestlik derecesi yönündeki kuvvetin büyüklüğüdür
ω, uyarım frekansıdır ve
γk, kuvvetin faz açısıdır.
Doğrusal sistemler için sistemin hareket denklemleri, n modal denklemine ayrıştırılır:
(Denklem 3).
{P} kuvvet vektörü (Denklem 3) ile değiştirildiğinde şu denklem ortaya çıkar:
(Denklem 4). Burada;
(Denklem 5)
(Denklem 4) için kararlı hal çözümü:
(Denklem 6).
(Denklem 6)'nın gerçek kısmı:
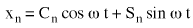(Denklem 7). Burada;
(Denklem 8) ve
(Denklem 9).
Yer değiştirme vektörü u, şu şekilde elde edilir:
(Denklem 10) veya
(Denklem 11)
kth serbestlik derecesi için uk yer değiştirme büyüklüğü ve karşılık gelen faz açısı θk:
(Denklem 12)
Hız ve ivme yanıtları, (Denklem 11) türevlerinden türetilir. Bunların genlikleri:
(Denklem 13)
Hız ve ivme faz açıları, yer değiştirme faz açılarına göre 90º ve 180º faz farkına sahiptir.