クリープは、一定の応力条件下で生じる時間依存の歪みです。
クリープはほとんどのエンジニアリング材料、特に高温の金属、高分子プラスチック、コンクリート、ロケット モーターの固形燃料などにおいてみられます。クリープ効果の発生には時間がかかるため、一般的 に、動解析ではその効果は無視されます。
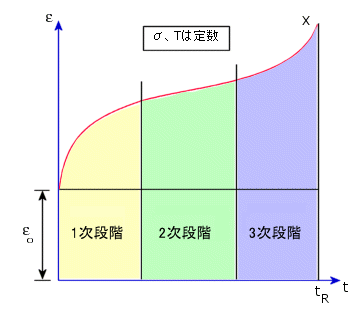
クリープ曲線は、歪みと時間のグラフです。クリープ曲線では、1 次、2 次、3 次の 3 つの異なる段階に区別できます。通常は、1次および2次段階が考慮されます。
「状態方程式」の方法に基づいた、クリープの従来の指数法則(Bailey-Norton 法則)が採用されます。 この法則は一軸応力および時間で、一軸クリープ歪みの方程式を定義します。