解析方法 - 不規則振動（Analysis Procedure - Random Vibration）

時変荷重によって動く線形 n 自由度系システムの運動方程式は次のようになります:

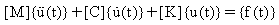(関係式 1)

座標変換を使用して、n 連立方程式を n 独立方程式（各方程式を独立して解くことができる）に変換します:

for r = 1, 2, ...., n （関係式 2）

ここで x_r(t) は節点座標 u_r(t) に次のように関連するモーダル座標です:

(関係式 3)

モーダル荷重 {m(t)} のベクトルは次で与えられます:

(関係式 4)

地盤振動が PSD 関数によって表現されているとして、解は周波数領域内で定式化されます。地盤振動 PSD 行列が [S_f(ω)] とされた場合、モーダル荷重 PSD 行列は次のように定義されます:

(関係式 5)

モーダル変位対応 [S_x(ω)] の PSD は次から得ます:

(関係式 6)

ここで [H(ω)] はモーダル伝達関数行列、そして [H*(ω)] はその共役複素数です。ノーマル モードでは、伝達関数行列は H_r(ω) によって対角行列要素となります。

（関係式 7）と

(関係式 8)

そして、変位応答 PSD [S_u(ω)] は（関係式 3）から導かれます。

(関係式 9)

速度と加速度の応答の PSD は次のように表現されます:

(関係式 10) と

(関係式 11)

モーダル速度と加速度 PSD はモーダル変位 PSD に次のように関連します:

(関係式 12) と (関係式 13)

（関係式 10）と（関係式 11）は次のように書き換えることができます:

(関係式 14) と (関係式 15)

モーダル応答 PSD を使用したゼロ遅延モーダル自己相関応答 (τ=0) は積分で計算されます:

(関係式 16)

(関係式 17)

(関係式 18)

上記の式から、平均2乗応答は対角行列要素によって決定されます:

(関係式 19)

(関係式 20)

(関係式 21)