조화 해석은 조화 하중에 대한 시스템의 정상상태 정점 응답 상태 반응을 평가합니다.
각 솔루션 스텝에서 모든 적용된 하중과 기저 가진에 동일한 진동수가 있습니다. 크기가 관련된 고유수 곡선으로 정의됩니다.
정의된 조화 절점 하중 벡터 {P}가 다음과 같을 경우:
(수식 1) 또는 
(수식 2),
여기에서,
Pk는 k번째 자유도 방향의 하중 크기입니다.
ω는 가진 진동수,
γk는 하중의 위상각입니다.
선형 시스템의 경우 시스템의 모션 수식이 모달 수식으로 분리됩니다.
(수식 3).
하중 벡터{P}를 (수식 3)으로 교체한 결과:
(수식 4), 여기에서
(수식 5)
(수식 4)의 정상 상태 이론해:
(수식 6).
(수식 6)의 실제 파트:
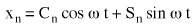(수식 7) 여기에서
(수식 8), 그리고
(수식 9).
변위 벡터 u는 다음 방정식으로 구해집니다.
(수식 10) 또는
(수식 11)
uk 변위 크기와 k번째 자유도의 해당 위상각 θk:
(수식 12)
속도와 가속도 반응이 (수식 11)의 도함수에서 파생됩니다. 폭:
(수식 13)
속도와 가속 위상각은 변위 위상각에 준하여 90º와 180º입니다.