시간 변위 하중으로 자극을 받은 선형 n 자유도 시스템의 모션 수식 시스템:
(수식 1)
여기에서,
[M] = n x n 대칭 관성 행렬
[C] = n x n 대칭 감쇠 행렬
[C] = n x n 상칭 강성 행렬
{f(t)} = n-차원 하중 벡터
{u},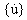 
, 
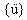은 차례로 변위, 속도, 가속 n-차원 벡터입니다.
(수식 1)은 일정 계수를 가진 n 미분 방정식 시스템입니다. 모션 수식은 질량, 강성, 감쇠 용어로 커플됩니다. 커플링은 모션 수식을 수학적으로 구사하는데 사용한 좌표계에 의존합니다.
모달 해석의 기본 개념은 (수식 1) 커플 시스템을 변형 매트릭스와 같은 모달 행렬[Φ]을 사용하여 한 쌍의 독립된 수식으로 변형하는 것입니다. [Φ]는 정상 모드 {f}i, i는 1, ....,n으로 다음과 같이 배치됨:
(수식 2)
정상 모드와 시스템의 고유치는 고유치 문제 해결에서 나옵니다.
(수식 3)
여기서 [ω2]는 고유진동수 제곱의 대각 행렬입니다.
선형 시스템의 경우, 모션의 n 수식 시스템은 모달 변위 벡터 {x} 차원에서 n 단일 자유도 수식으로 분리될 수 있습니다.
(수식 4)
(수식 4)에서 벡터 {u}를 빼고 이 값을 [Φ]T(수식 1)으로 곱하여 다음을 얻습니다.
(수식 5)
정상 모드는 직교성을 만족하고, 모달 행렬 [Φ]는 다음 수식을 만족하도록 정규화됩니다.
(수식 6)
(수식 7), 그리고
(수식 8).
(수식.6--8)으로 대체하면, (수식 5)는 n SDOF 2차 미분 방정식이 됩니다.
여기서 i =1, ..., n(수식 9)
(수식 9)은 Wilson-Theta와 Newmark 같은 단계별 통합 메서드를 사용하여 해결됩니다.
이 때, 통합은 시간 도메인에서 행해집니다. 즉, 최종 스텝 결과는 다음 스텝 결과 예상에 사용되어집니다.
시스템 변위 벡터(u)는 (수식 4)에서 비롯됩니다.