Оптимизация топологии является наиболее распространенным типом структурной оптимизации. Она используется в начальной фазе проектирования для прогнозирования оптимального распределения материала в рамках указанного исходного пространства проектирования структуры и рассматривает функциональные спецификации и производственные ограничения.
Наиболее популярным математическим методом для оптимизации топологии является метод твердого изотропного материала с пенализацией (SIMP). Метод SIMP был изначально предложен Бендсо и Кикучи (Bendsoe, Kikuchi) (1988) и Розваны и Чжоу (Rozvany, Zhou) (1992). Метод SIMP прогнозирует оптимально распределение материалов в пределах указанного проектного пространства для представленных случаев нагрузок, граничных условий, производственных ограничения и требований производительности.
В соответствии с
Бендсо (Bendsoe) (1989):
"Оптимизация формы в самом общем смысле должна включать в себя определение для каждой точки в пространстве вне зависимости от нахождения материала в данной точке". Традиционный подход к оптимизации топологии — это разделение области на сетку конечных элементов, которая называется изотропной сплошной микроструктурой. Каждый элемент заполняется материалом для областей, которым требуется материал, или не содержит материала для областей, где можно удалять материал (представление пустот). Распределение плотности материала в рамках проектного домена, ρ, является дискретным, а каждому элементу назначается двоичное значение:
-
ρ(e) = 1, где требуется материал (черный)
- ρ(e) = 0, где материал удален (белый)
Например, на изображении представлен оптимизированный макет материала загруженного пучка. Твердые элементы с плотностью ρ(e) =1 являются черными, пустые элементы с ρ(e) = 0 удалены.
Представление постоянной функции распределения относительной плотности избегает появления двоичных ошибок двухпозиционной природы. Для каждого элемента назначенная относительная плотность может отличаться между минимальным значением ρmin и 1, что позволяет назначать элементам промежуточные плотности (характеризуются как пористые элементы):
ρmin — это минимальное допустимое значение относительной плотности для пустых элементов больше нуля. Данное значение плотности обеспечивает числовую стабильность анализа конечных элементов.
Поскольку относительная плотность материала может непрерывно меняться, модуль Юнга материала на каждом элементе может также постоянно меняться. Для каждого элемента "e" представляет собой связь между коэффициентом относительной плотности материала ρ
e и модулем Юнга для упругости, назначенной изотропной модели материала Ε
0, что вычисляется степенным законом:
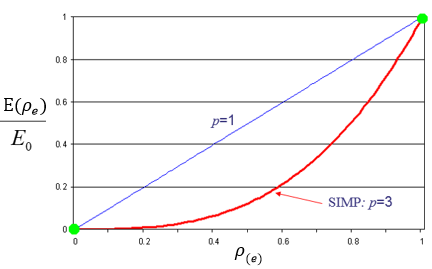
Поправка на потери p снижает вклад элементов с промежуточными плотностями (серые элементы) до общей жесткости. Поправка на потери контролирует решение оптимизации для элементов, которые представлены сплошным черным (ρe = 1) или пустым белым (ρe= ρmin). Численные эксперименты показывают, что подходит значение поправки на потери p = 3.
Уменьшение модуля эластичности материала элемента ведет к уменьшению жесткости элемента. С учетом метода SIMP глобальная жесткость модулируется в соответствии с:
где
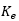
— это матрица жесткости элемента, ρ
min представляет собой минимальную относительную жесткость, ρ
e является относительной плотностью элемента, p — поправка на потери, а N — количество элементов в домене проектирования.
Например, для элемента с назначенной относительной плотностью ρe = 0,5, поправка на потери = 3, а ρmin = 0,001, глобальная матрица жесткости масштабируется коэффициентом (0,001 + (1 -0,001)* 0,5 ^3) = 0,12587.
Целевая функция: Предельное увеличение жесткости
Популярная цель оптимизации заключается в максимальном увеличении общей жесткости структуры или минимизации ее податливости при удалении указанного объема массы.
Податливость — это показатель общей гибкости или мягкости структуры, который является обратной величиной жесткости. Глобальные условия податливости равны сумме упругости элементов или энергий деформации. Минимизация глобальной податливости (C) эквивалентна максимизации глобальной жесткости. Алгоритм оптимизации посредством итеративного процесса старается разрешить значения плотности элементов (которые являются расчетными переменными оптимизации), которые минимизируют глобальную податливость структуры.
[ue] — это вектор узлового перемещения элемента e, [Ke] представляет собой жесткость элемента e, а вектор {ρ} содержит значения относительной плотности элемента ρe.
Во время каждой итерации оптимизации должны быть удовлетворены целевое ограничение массы, глобальное равновесие силы и жесткости и требуемые функциональные ограничения:
v
e является объемом элемента, а M
target представляет собой целевую массу оптимизации.
[K{
ρ}] — глобальная матрица жесткости, смодулированная вектором относительной плотности, {u} — это вектор смещения, а {F} является вектором внешней силы.
Формула выше содержит ограничения отклика проектирования, например предельные значения напряжения, смещения, собственные частоты и т. д.
Анализ чувствительности
Во время каждой итерации алгоритмы оптимизации выполняют анализ чувствительности для оценки влияния разновидностей плотности материала на целевые показатели с целью максимального повышения жесткости.
Математически, анализ чувствительности выражается как производная от целевой функции относительно плотности материала:
Во время анализа чувствительности элементы, взвешенные с низкими коэффициентами плотности материала, в конечном итоге теряют свою структурную релевантность и исключаются в ходе последующих итераций.
При расчете чувствительности для каждого независимого элемента и без учета подключения между элементами это может привести к разрыву материала и к отключению объемов от основной геометрии. Это известно как эффект "шахматной доски". Для снижения эффекта "шахматной доски" для схемы фильтрации применяются радиус влияния элемента и усреднение значения чувствительности каждого элемента внутри его области влияния.
Итерации оптимизации продолжаются до схождения различий целевой функции и достижения итерациями их критерия сходимости.