Düzensiz titreşim ortamında çalışan bileşenler için yorulma hasarı değerlendirmesi, yanıt gerilimi güç spektral yoğunluğu (PSD) fonksiyonunun istatistiksel özelliklerine göre frekans etki alanında tahmin edilir.
Yapılar veya mekanik bileşenler rüzgar yükü altındaki bir rüzgar türbini, dalga yükü altındaki bir kıyıdan uzak yapı veya farklı yol yüzeyi profillerinde çalışan bir araba motoru gibi rastgele bir yükleme şekline maruz kaldığında, yorulma ömrü tahminleri frekans etki alanında yapılır.
Titreşim yorulması (veya frekansa bağlı yorulma) terimi yükleme ve yanıtın (gerilim ve gerinim geçmişleri) rastgele işlemler olduğu, dolayısıyla en iyi şekilde Güç Spektral Yoğunluğu (PSD fonksiyonları) gibi istatistiksel ölçüler kullanılarak açıklanabileceği durumlarda yorulma ömrü tahminini ifade eder.
Yanıt gerilimi PSD'nin istatistiksel karakteristikleri PSD fonksiyonunun momentlerinden elde edilebilir.
| PSD'nin İstatistiksel Özellikleri |
Denklem |
|---|
| f frekansında (Hz biriminde) gerilim PSD'sinin n.spektral momenti. |
 (Denk.1) (Denk.1)
|
| Sürekli bir sabit Gauss sürecinin σ ortalama karekök değeri. |
 (Denk.2) (Denk.2)
|
| Tipik 1 saniyelik örnek için yukarı doğru sıfırdan geçişlerin ortalama sayısı E[0]. |
 (Denk.3) (Denk.3)
|
| Tipik 1 saniyelik örnek için ortalama tepe sayısı E[p]. |
 (Denk.4) (Denk.4)
|
| y düzensizlik faktörü 0 ile 1 arasında değişir. Stres sinyali dar bir bant sürecine yaklaştığında 1'e yaklaşır (sinüs dalgası için y =1). Stres sinyali beyaz gürültü sürecine yaklaştığında 0'a yaklaşır. |
 (Denk.5) (Denk.5)
veya
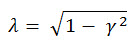 (Denk.6) (Denk.6)
|
Malzeme yorulma özellikleri, genellikle bir S-N eğrisinden elde edilir; bu eğri gerilim aralığı S (bu, gerilim halindeki maksimum döngüsel gerilim ile sıkıştırma halindeki minimum döngüsel gerilim arasındaki gerilim farkıdır) ile arızaya kadar geçen ortalama döngü sayısı N arasındaki ilişkiyi tanımlar.
Çoğu yüksek döngülü yorulma probleminde (N >= 104 ), S-N eğrisi basitleştirilmiş şekilde ifade edilebilir:
 (Denk.7)
(Denk.7)
burada B ve m, yükleme ve ortam koşullarına göre değişen malzeme özellikleridir ve yorulma testi deneyleriyle belirlenir.
Rastgele yüklemeye bağlı yorulmadan kaynaklanan toplam hasar E[AD] Palmgren-Miner kuralına dayanır ve şu şekilde ifade edilir:
 (Denk.8)
(Denk.8)
burada n(S), gerilim aralığı düzeyi S'de uygulanan döngü sayısı; p(S) ise gerilim aralığının olasılık yoğunluk fonksiyonudur. Yukarıdaki denklemi yerine basitleştirilmiş S-N eğrisi denklemi kullanıldığında aşağıdakilerden genel bir rastgele gerilim yanıtına bağlı yorulma hasarı denklemi elde edilir:
 (Denk.9); burada T rastgele yüklemenin sn cinsinden süresidir.
(Denk.9); burada T rastgele yüklemenin sn cinsinden süresidir.
Yorulma hasarı tahmini için Denk.9'a dayanan üç yöntem vardır: Steinberg üç bant yöntemi, Dar bant yöntemi ve Wirshing yöntemi. Her yöntemde olasılık yoğunluk fonksiyonu p(S) için farklı bir tanım kullanılır.
Dar Bant yöntemi
Dar bant yönteminde, dar bant sinyali için tepelerin olasılık yoğunluk fonksiyonu bir Rayleigh dağılımına eğilim gösterir (Bendat J.S., Probability Functions for Random Responses. NASA report on Contact NASA-5-4590, 1964).
 (Denk.10)
(Denk.10)
(Denk.10)'un (Denk.9) yerine kullanılması ve entegre edilmesi, yorulma hasarı tahmininde aşağıdaki ifadeyle sonuç verir.
 (Denk.11); burada Γ(.) Gamma fonksiyonudur.
(Denk.11); burada Γ(.) Gamma fonksiyonudur.
Wirsching yöntemi
Wirsching yöntemi (Wirshing, P.H., Paez, T.L., and Ortiz K., Random Vibration, John Wiley & Sons Inc., New York, 1995), Dar Bant yöntemini geniş bant sürecini göz önünde bulunduracak şekilde ampirik bir düzeltme faktörüyle değiştirir.
 (Denk. 12)
(Denk. 12)
 , (Denk. 13)
, (Denk. 13)
ζw, çeşitli spektral yoğunluk fonksiyonları içeren Monte Carlo simülasyonlarından elde edilmiş ampirik bir faktördür.
αw ve bw aşağıdakilerden elde edilen en uygun parametrelerdir:
 (Denk. 14)
(Denk. 14)
Steinberg üç bant yöntemi
Steinberg yöntemi, rastgele gerilim yanıtının olasılık yoğunluk fonksiyonunun bir Gauss dağılımını izlediği, bu nedenle beklenen gerilim yanıtı genlik değerlerinin belirli olasılık düzeylerine bağlı olduğu varsayımına dayanır:
- Stres döngüleri genliğinin gerilim yanıtı sinyalinin ortalama karekökünün 2 katı aralığını aşmama olasılığı %68,27'dir.
- Stres döngüleri genliğinin gerilim yanıtı sinyalinin ortalama karekökünün 4 katı aralığını aşmama olasılığı %27,1'dir.
- Stres döngülerinin gerilim yanıtı sinyalinin ortalama karekökünün 6 katı aralığını aşmama olasılığı %4,3'tür.
Ortalama karekökün 6 katından büyük aralıklarda gerilim döngüsü gerçekleşmez.
Beklenen yorulma hasarı şu denklemle elde edilir:
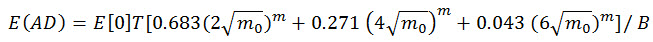 (Denk.15)
(Denk.15)
Simulation'da gerilim PSD fonksiyonları, yorulma etüdünün dayandığı dinamik - düzensiz titreşim etüdünden elde edilen sonuçlardır. Üç yöntemde de yorulmaya bağlı olarak beklenen hasarın hesaplanmasında Stres (von Mises) bileşeni göz önünde bulundurulur.