Harmonická analýza vyhodnocuje špičkovou odezvu systému v ustáleném stavu vzhledem k harmonickému zatížení.
Při každém kroku řešení mají všechna použitá zatížení a základová buzení stejnou frekvenci. Velikosti jsou definovány přidruženými frekvenčními křivkami.
Uvažujme vektor harmonické uzlové síly {P} definovaný jako:
 (rovnice 1) nebo
(rovnice 1) nebo  (rovnice 2),
(rovnice 2),
kde:
Pk je velikost síly ve směru k-tého stupně volnosti
ω je frekvence buzení
a γk představuje fázový úhel síly.
U lineárních systémů se rovnice pohybu v systému rozdělí do n modálních rovnic:
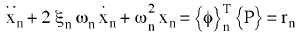 (rovnice 3).
(rovnice 3).
Dosazením vztahu pro vektor síly {P} do rovnice 3 získáme tento tvar:
 (rovnice 4), kde
(rovnice 4), kde
 (rovnice 5)
(rovnice 5)
Řešením ustáleného stavu u rovnice 4 je:
 (rovnice 6).
(rovnice 6).
Reálná část rovnice 6 je:
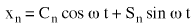 (rovnice 7), kde
(rovnice 7), kde
 (rovnice 8) a
(rovnice 8) a
 (rovnice 9).
(rovnice 9).
Vektor posunutí u je dán tímto vztahem:
 (rovnice 10) nebo
(rovnice 10) nebo
 (rovnice 11)
(rovnice 11)
Velikost posunutí uk a odpovídající fázový úhel θk pro k-tý stupeň volnosti jsou:
 (rovnice 12)
(rovnice 12)
Reakce rychlosti a zrychlení jsou odvozeny z odvozenin rovnice 11. Jejich amplitudy jsou:
 (rovnice 13)
(rovnice 13)
Fázové úhly rychlostí a zrychlení jsou 90 º a 180 º vzhledem k fázovým úhlům posunutí.