Systémy s jedním stupněm volnosti (SDOF)
Uvažujte jednoduchý systém hmoty a pružiny. Hmota (m) je vystavena působení síly F(t) ve směru u jako funkce času. Hmota se může pohybovat pouze ve směru u, a proto se jedná o systém s jedním stupněm volnosti (SDOF). Pohybu klade odpor pružina o tuhosti (k)
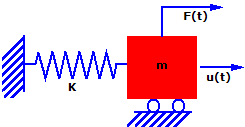
Zápisem druhého Newtonova zákona (síla = hmotnost x zrychlení) pro tento systém v čase (t) získáme:
F(t)-ku(t) = mu..(t)
nebo:
mu..(t) + ku(t) = F(t)
kde:
u..(t) je zrychlení hmoty v čase (t) a je rovno druhé derivaci u vzhledem k času
k = tuhost pružiny
Pokud dojde k posunutí a uvolnění hmoty, bude teoreticky dále neustále vibrovat se stejnou amplitudou. V praxi však hmota vibruje se stále menší amplitudou, dokud nepřejde do klidového stavu. Tento jev se nazývá tlumení a je způsoben ztrátou energie třením a dalšími účinky. Tlumení je složitý jev. Pro účely této diskuse předpokládejme, že je síla tlumení poměrná k rychlosti. Tento typ tlumení se nazývá viskózní tlumení.
Pokud uvažujeme tlumení, získáme z rovnice výše následující vztah:
mu..(t) + cu.(t) + ku(t) = F(t)
kde:
u.(t) je rychlost hmoty v čase (t) a je rovna první derivaci u vzhledem k času
Ve statických studiích jsou rychlosti a zrychlení tak malé, že je lze zanedbat, a F a u nejsou funkcemi času. Rovnice výše se zjednoduší na: F=ku.
Systémy s více stupni volnosti (MDOF)
V systémech s více stupni volnosti (MDOF) se m, c a k stanou maticemi (místo jediných hodnot) a rovnice pohybu jsou vyjádřeny takto:
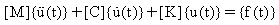
kde:
[M]: matice hmoty
[K] : matice tuhosti
[C] : matice tlumení
{u(t)}: vektor posunutí v čase t (součásti posunutí každého uzlu)
: vektor zrychlení v čase t (součásti zrychlení každého uzlu)
: vektor rychlosti v čase t (součásti rychlosti každého uzlu)
{f(t)}: časově proměnný vektor zatížení (součásti síly každého uzlu)