I materiali elastici con capacità di dissipare l'energia meccanica a causa di effetti viscosi sono noti come materiali viscoelastici.
Per lo stato di sollecitazione multiassiale, la relazione costitutiva può essere scritta come:

dove: e(bar) e φ sono deformazioni deviatoriche e volumetriche, G(t - τ) e K(t - τ) sono le funzioni di rilassamento di taglio e dell'ambiente circostante.
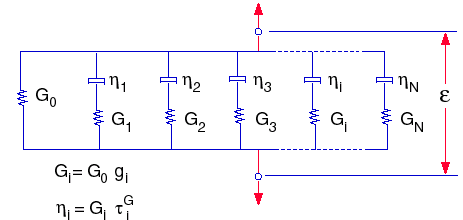
Le funzioni di rilassamento possono essere rappresentate da un modello meccanico, generalmente denominato Modello Maxwell generalizzato, con le espressioni:

dove: G0 = E / 2(1+ ν), modulo di taglio iniziale (t=0)
e K0= E / 3(1 -2ν), modulo iniziale dell'ambiente circostante (t=0)
gi, ki, τi
G e τi
K sono i moduli iniziali di rilassamento di taglio e dell'ambiente circostante e i tempi corrispondenti.
L'effetto della temperatura sul comportamento del materiale è introdotto attraverso il principio di corrispondenza tempo-temperatura. La formula matematica del principio è:

dove γt è il tempo ridotto e γ è la funzione di variazione. L'equazione WLF (Williams-Landel-Ferry) è utilizzata per l'approssimazione della funzione:

dove T0 è la temperatura di riferimento che solitamente viene usata come temperatura di transizione vetrosa; C1 e C2 sono costanti che dipendono dal materiale.
| Parametro |
Proprietà del materiale |
|---|
| Parametri elastici lineari |
Modulo elastico in X
|
|
Coefficiente di Poisson in XY
|
|
Modulo di taglio in XY
|
| Parametri della funzione di rilassamento |
Modulo di rilassamento di taglio (da 1 a 8) (rappresentano g1, g2, ..., g8 nelle equazioni del Modello Maxwell generalizzato)
|
|
Valori temporali (Modulo di rilassamento di taglio da 1 a 8) (rappresentano τ1
g, τ2
g, ..., τ8
g nelle equazioni del Modello Maxwell generalizzato) |
|
Modulo di rilassamento dell'ambiente (da 1 a 8) |
|
Valori temporali (Modulo di rilassamento dell'ambiente circostante da 1 a 8) (rappresentano τ1
k, τ2
k, ..., τ8
k nelle equazioni del Modello Maxwell generalizzato) |
| Parametri dell'equazione WLF
|
Temperatura di transizione vetrosa
(rappresenta T0 nell'equazione WLF)
|
|
Prima costante per l'equazione Williams-Landel-Ferry
(rappresenta C1 nell'equazione WLF)
|
|
Seconda costante per l'equazione Williams-Landel-Ferry
(rappresenta C2 nell'equazione WLF)
|
durante la definizione di una curva di rilassamento di taglio o dell'ambiente nella tabella Tabelle e curve, il primo punto della curva è il modulo G1 o K1 nel tempo 1. Al momento t = 0, il programma calcola automaticamente G0 o K0 dal Modulo elastico e dal rapporto di Poisson.
Il modello del materiale viscoelastico può essere utilizzato con elementi solidi e di shell spesso di qualità bozza o alta.
Il tempo ha un valore reale nell'analisi non lineare quando si usa il modello del materiale viscoelastico.