応力周期に対する交番応力の振幅は、周期内の応力範囲の1/2で計算されます。応力サイクルによる損傷量は、代替応力だけでなく、平均応力にも依存します。たとえば、下記の2つの周期は同一の交番応力を有していますが、平均応力が異なるため、異なる損傷量が生じます。
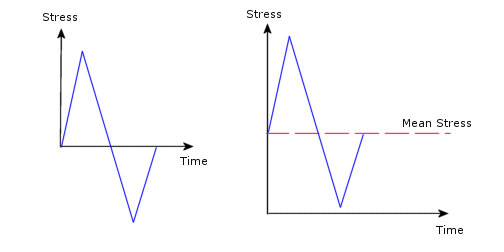
破壊に対するサイクルの平均応力の影響は、次の Haigh 図に示されています。
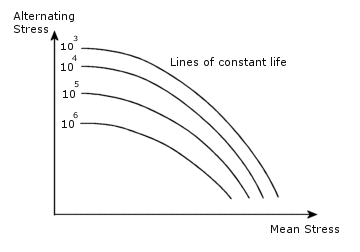
平均応力は、荷重が完全可逆である場合のみゼロになります。 最も簡単なケースは、同一の R 比による S-N カーブが荷重として与えられる場合です。 この場合の S-N カーブは補正を必要としないため、直接的に使用されます。 異なる R 比により S-N カーブを定義した場合、ソフトウェアはカーブ間の線形補間により平均応力を考慮します。 荷重の R 比と異なる R 比による S-N カーブが 1 つだけ提供される場合には、補正が必要となります。
プログラムは、平均応力の計算に常に von Mises 応力を使用します。 Von Mises は、正の結果量のため、関連する平均応力を計算する目的で代数的に最大の主応力の符合が割り当てられます。
定義
補正手法を説明するにあたり、応力周期に対して以下の変数を定義します:
Smax = 最大応力
Smax = 最小応力
ΔS = 応力範囲 = Smax - Smin
Sa = 交番応力 = (Smax - Smin)/2
Smean = 平均応力 = (Smax + Smin)/2
R = 応力比 = Smin/Smax
A = 振幅比 = Sa/Smean
一般的な荷重に対する応力比および振幅比を以下に示します:
| 荷重タイプ
|
応力および振幅比
|
| 完全な反転
|
R = -1、A = 無限
|
| ゼロから最大
|
R = 0、A = 1
|
| ゼロから最小
|
R = 無限、A = -1
|
補正手法(Correction methods)
次を行います。
Sca = 補正済み交番応力(ゼロ平均に基づいて)、
Sy = 降伏応力、および
Su = 極限応力
このソフトウェアで S
ca の計算に使用できる手法は次のとおりです。
| 方法
|
方程式
|
| 1. Goodman 手法 - 一般的に脆性材料に適しています。
|
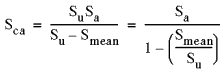
|
| 2. Gerber 手法 - 一般的に延性材料に適しています。
|
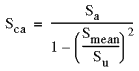
|
| 3. Soderberg 手法 - 一般的に最も無難な手法です。
|
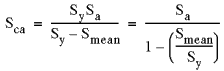
|
変動および一定振幅イベントの双方に対して、ソフトウェアは各周期の交番応力に加えて平均応力を計算し、指定条件を用いた補正済み応力の評価を行います。