응력 싸이클의 교번응력이 싸이클의 응력 영역의 1/2로 계산됩니다. 응력 싸이클로 인한 손상도는 교차 응력뿐만 아니라 평균 응력에 따라 다릅니다. 예를 들어, 아래의 두 싸이클에 같은 교차 응력이 있으나 평균 응력이 다르므로, 손상도가 다릅니다.

Haigh 도표로 불리우는 다음 도표는 싸이클의 평균 응력이 실패에 주는 영향을 보여줍니다.

하중이 완전 역방향일 경우에만 평균 응력이 0 입니다. 하중과 같은 R-비가 있는 S-N 곡선이 제공된 경우가 대표적입니다. 이 경우, 수정이 필요 없으므로 S-N 곡선이 직접 사용됩니다. 다른 R 비율로 S-N 곡선을 정의하면, 곡선 사이의 선형 보간법으로 평균 응력을 고려합니다. 로딩하는 R-비율과 다른 R-비율의 S-N 곡선 하나만 제공되면 수정이 필요합니다.
평균 응력 계산에는 항상 von Mises 응력이 사용됩니다. von Mises가 양수의 수량일 때, 연관 평균 응력 계산을 목적으로 주응력 기호가 최대 대수로 지정됩니다.
정의
수정 방법을 설명하기 위해, 응력 싸이클의 변수를 다음과 같이 정의하겠습니다.
Smax = 최대 응력
Smin = 최소 응력
ΔS = 응력 영역 = Smax - Smin
Sa = 교차 응력 = (Smax - Smin)/2
Smean = 평균 응력 = (Smax + Smin)/2
R = 응력 비율 = Smin/Smax
A = 폭 비율 = Sa/Smean
일부 공통 하중의 응력과 폭 비율이 표시됩니다.
| 하중 유형
|
응력과 폭 비율
|
| 역방향
|
R = -1, A = 무한
|
| 0 에서 최대값까지
|
R = 0, A = 1
|
| 0 에서 최소값까지
|
R = 무한, A = -1
|
수정 방식
다음과 같이 합니다.
ca = 수정된 교번 응력 (0 평균 기반),
Sy = 항복 응력,
Su = 극한 응력
S
ca 계산을 위해 다음 방식이 제공됩니다.
| 방식
|
수식
|
| 1. Goodman - 일반적으로 파손되기 쉬운 재질에 적합합니다.
|

|
| 2. Gerber 방식 - 일반적으로 연성 재질에 적합합니다
|
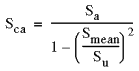
|
| 3. Soderberg 방식 - 일반적으로 가장 무난한 방식입니다
|

|
부동 진폭 이벤트와 가변 진폭 이벤트 모두에, 각 싸이클에 대한 교번응력과 더불어 평균응력이 계산된 후 지정한 방법을 통해 수정된 응력이 계산됩니다.