Analiza harmoniczna oszacowuje szczytową reakcję układu w stanie ustalonym na obciążenia harmoniczne.
W każdym kroku rozwiązania wszystkie zastosowane obciążenia i wzbudzenia podstawowe mają tą samą częstotliwość. Wielkości są definiowane przez skojarzone krzywe częstotliwości.
Załóżmy harmoniczny wektor węzłowy siły {P} zdefiniowany jako:
(Równanie 1) lub 
(Równanie 2),
gdzie:
Pk jest wielkością siły w kierunku k-tego stopnia swobody,
ω jest częstotliwością wzbudzającą,
natomiast γk jest kątem fazowym siły.
Dla układów liniowych, równania ruchu układu są rozprzężone do n równań modalnych:
(Równanie 3).
Podstawiając wektor siły {P} do (Równania 3) otrzymujemy:
(Równanie 4), gdzie:
(Równanie 5)
Rozwiązanie stanu ustalonego dla (Równania 4):
(Równanie 6).
Część rzeczywista (Równania 6):
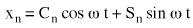(Równanie 7), gdzie:
(Równanie 8) i
(Równanie 9).
Wektor przemieszczenia:
(Równanie 10) lub
(Równanie 11)
Wielkość przemieszczenia uk i odpowiedni kąt fazowy θk dla k-tego stopnia swobody:
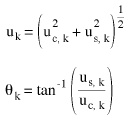(Równanie 12)
Reakcje prędkości i przyspieszenia są wyprowadzone z pochodnych (Równania 11). Ich amplitudy:
(Równanie 13)
Kąty fazowe prędkości i przyspieszeń są przesunięte o 90º i 180º względem kątów fazowych przemieszczenia.