|
Maximálnà hodnoty modálnà odezvy
|
NechĹĄ Sd(ωI, ÎľI), Sv(ωI, ÎľI) a Sa(ωI, ÎľI) jsou vstupnĂ hodnoty spektra odezvy pro posun, pseudorychlost, respektive pseudozrychlenĂ. ProtoĹľe je moĹľnĂ© kaĹľdĂ˝ reĹľim idealizovat jako systĂ©m s jednĂm stupnÄ›m volnosti, maximálnĂ odezvy pĹ™es trvánĂ buzenĂ ve smyslu modálnĂch souĹ™adnic ze vstupnĂch hodnot spektra odezvy:

 jsou modálnà relativnà posuny, jsou modálnà relativnà posuny,
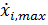 modálnà relativnà rychlosti a modálnà relativnà rychlosti a
 modálnà absolutnà akcelerace. modálnà absolutnà akcelerace.
Γi je modálnĂ faktor podĂlu pro kaĹľdĂ˝ reĹľim i, kterĂ˝ je roven  . .
 transpozice vlastnĂho vektoru i. transpozice vlastnĂho vektoru i.
 , kterĂ˝ je vektorem pĹŻsobenĂ, kterĂ˝ se vztahuje k základovĂ©mu pohybu strukturálnĂch posunĹŻ pevnĂ©ho tÄ›lesa. , kterĂ˝ je vektorem pĹŻsobenĂ, kterĂ˝ se vztahuje k základovĂ©mu pohybu strukturálnĂch posunĹŻ pevnĂ©ho tÄ›lesa.
Pro kaĹľdĂ˝ reĹľim jsou maximálnĂ odezvy struktury ve vztahu k modálnĂm souĹ™adnicĂm: 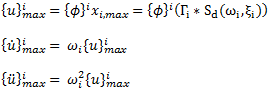
|