Posouzení poškození v důsledku únavy pro součásti, které jsou provozovány v prostředí s náhodnými vibracemi, se odhaduje ve frekvenční doméně na základě statistických vlastností funkce spektrální hustoty výkonu (PSD) napětí odezvy.
Když jsou konstrukce nebo mechanické součásti vystaveny náhodné formě zatížení, například větrná turbína v náporu větru, příbřežní konstrukce zatížená vlnami nebo motor auta provozovaný na různých profilech silničních povrchů, provádějí se odhady únavové životnosti ve frekvenční doméně.
Termín únava z vibrací (nebo únava na základě frekvence) odkazuje na odhad únavové životnosti , kde zatížení a odezva (historie napětí a namáhání) jsou náhodné procesy, a proto se nejlépe popisují pomocí statistických měr jako spektrální hustota výkonu (funkce PSD).
Statistické charakteristiky PSD napětí odezvy lze získat prostřednictvím momentů funkce PSD.
| Statistické charakteristiky PSD |
Rovnice |
|---|
| N-tý spektrální moment PSD napětí S(f) při frekvenci f (v jednotkách Hz). |
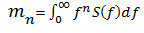 (rovnice 1) (rovnice 1)
|
| Efektivní hodnota pro nepřetržitý stacionární Gaussův proces σ. |
 (rovnice 2) (rovnice 2)
|
| Průměrný počet průchodů nulou směrem vzhůru E[0] pro typický vzorek 1 sekundy. |
 (rovnice 3) (rovnice 3)
|
| Průměrný počet vrcholů E[p] pro typický vzorek 1 sekundy. |
 (rovnice 4) (rovnice 4)
|
| Činitel nepravidelnosti γ kolísá mezi 0 a 1. Blíží se 1, když se signál napětí blíží procesu úzkopásmové metody (pro sinusovou křivku γ =1). Blíží se 0, když se signál napětí blíží procesu bílého šumu. |
 (rovnice 5) (rovnice 5)
nebo
 (rovnice 6) (rovnice 6)
|
Vlastnosti únavy materiálu jsou obvykle získávány z křivky S-N, která definuje vztah mezi rozsahem napětí S (jedná se o kolísání napětí od maximálního cyklického napětí v tahu po minimální cyklické napětí ve stlačení) a průměrným počtem cyklů do selhání N.
Pro většinu problémů vysokocyklové únavy (N >= 104 ) lze křivku S-N vyjádřit ve zjednodušené podobě:
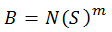 (rovnice 7)
(rovnice 7)
kde B a m jsou vlastnosti materiálu měnící se podle zatížení a podmínek prostředí a jsou zjišťovány pomocí experimentů testování únavy.
Kumulované poškození E[AD] kvůli únavě z náhodného zatížení je založeno na Palmgren-Minerově pravidle a je vyjádřeno takto:
 (rovnice 8)
(rovnice 8)
kde n(S) je počet cyklů použitých při úrovni rozsahu napětí S a p(S) je funkce hustoty pravděpodobnosti rozsahu napětí. Dosazením rovnice zjednodušené křivky S-N v rovnici výše získáme obecnou rovnici poškození v důsledku únavy z náhodné odezvy napětí z této rovnice:
 (rovnice 9), kde T je doba trvání náhodného zatížení v sekundách.
(rovnice 9), kde T je doba trvání náhodného zatížení v sekundách.
K dispozici jsou tři metody pro odhad poškození v důsledku únavy na základě rovnice 9: Steinbergova třípásmová metoda, úzkopásmová metoda a Wirshingova metoda. Každá metoda používá jinou definici pro funkci hustoty pravděpodobnosti p(S).
Úzkopásmová metoda
V úzkopásmové metodě funkce hustoty pravděpodobnosti vrcholů pro úzkopásmový signál směřuje k Rayleigho rozdělení (Bendat J.S., Probability Functions for Random Responses. Zpráva NASA v Contact NASA-5-4590, 1964).
 (rovnice 10)
(rovnice 10)
Dosadíme (rovnici 10) v (rovnici 9) a integrujeme výsledky do následujícího výrazu pro odhad poškození v důsledku únavy.
 (rovnice 11), kde Γ(.) je gama funkce.
(rovnice 11), kde Γ(.) je gama funkce.
Wirschingova metoda
Wirschingova metoda (Wirshing, P.H., Paez, T.L. a Ortiz K., Random Vibration, John Wiley & Sons Inc., New York, 1995) upravuje úzkopásmovou metodu pomocí empirického faktoru korekce a bere v úvahu širokopásmový proces.
 (rovnice 12)
(rovnice 12)
 , (rovnice 13
, (rovnice 13
ζw je empirický faktor odvozený ze simulací Monte Carlo, které zahrnují celou řadu funkcí spektrální hustoty.
αw a bw jsou nejvhodnější parametry získané z:
 (rovnice 14
(rovnice 14
Steinbergova třípásmová metoda
Předpokladem Steinbergovy třípásmové metody je, že funkce hustoty pravděpodobnosti náhodné odezvy napětí má Gaussovo rozložení, a proto jsou očekávané hodnoty amplitud odezvy napětí ohraničeny určitými úrovněmi pravděpodobnosti:
- 68,27% šance, že amplituda cyklů napětí nepřesáhne rozsah dvojnásobku efektivní hodnoty signálu odezvy napětí.
- 27,1% šance, že amplituda cyklů napětí nepřesáhne rozsah čtyřnásobku efektivní hodnoty signálu odezvy napětí.
- 4,3% šance, že cykly napětí nepřesáhnou rozsah šestinásobku efektivní hodnoty signálu odezvy napětí.
Nevyskytují se cykly napětí s rozsahy většími než šestinásobek efektivní hodnoty.
Očekávané poškození v důsledku únavy je dáno rovnicí:
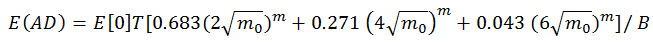 (rovnice 15)
(rovnice 15)
V softwaru Simulation jsou funkce PSD napětí výsledkem dynamické studie náhodných vibrací, na které je studie únavy založena. Pro všechny tři metody je pro výpočet očekávaného poškození v důsledku únavy uvažována součást napětí von Mises.