Na análise estática linear, as cargas são aplicadas lenta e gradativamente até atingirem suas magnitudes totais. Após atingirem a magnitude total, as cargas permanecem constantes (não variam com o tempo). As acelerações e velocidades do sistema excitado são desprezíveis e, portanto, nenhuma força inercial ou de amortecimento é considerada na fórmula:
onde:
[K] : matriz de rigidez
{u}: vetor de deslocamento
F: vetor de carga.
A solução produz deslocamentos e tensões constantes.
Na análise dinâmica linear, as cargas aplicadas dependem do tempo. As cargas podem ser determinísticas (periódicas, não periódicas) ou não determinísticas, significando que não podem ser previstas com precisão, mas podem ser descritas estatisticamente. As acelerações e velocidades do sistema excitado são significativas e, portanto, as forças inerciais e de amortecimento devem ser consideradas na fórmula:
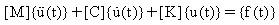
onde:
[K] : matriz de rigidez
[C] : matriz de amortecimento
-M matriz de massa
{u(t)}: vetor de deslocamento com variação no tempo
vetor de aceleração com variação no tempo
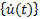: vetor de velocidade com variação no tempo
{f(t)}: vetor de carga com variação no tempo
A resposta do sistema é obtida em termos de histórico de tempo (amplitudes em relação ao tempo) ou em termos de espectro de frequência (valores de pico em relação à frequência).
Na análise dinâmica linear, as matrizes de massa, rigidez e amortecimento não variam com o tempo.
As as propriedades do material são consideradas lineares. Os estudos dinâmicos não lineares devem ser usados se existir uma não linearidade do material.
Em geral, você pode supor condições estáticas se a frequência das cargas for muito menor do que a menor frequência natural do sistema.