由随时间变化的力所激发的线性 n 自由度系统的运动方程式系统为：
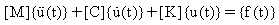（方程式 1）
其中：
[M] = n x n 对称惯性矩阵
[C] = n x n 对称阻尼矩阵
[K] = n x n 对称刚度矩阵
{f(t)} = n 维力向量
{u}、
和 
分别是位移、速度和加速度 n 维向量。
（方程式 1）是一组具有常量系数的 n 阶联立常微分方程式。运动方程式由质量、刚度和阻尼这几个条件组合而成。组合取决于用来以数学方式描述运动方程式的坐标系。
模态分析的基本思想是通过将模态矩阵 [Φ] 用作转换矩阵，从而将（方程式 1）连接的系统转换为一组独立的方程式。[Φ] 包含正常模式 {f}i (i = 1, ....,n)，其排列方式为：
（方程式 2）
系统的正常模式和特征值通过解决特征值问题而得出：
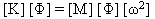（方程式 3）
其中 [ω2] 是固有频率平方的对角矩阵。
对于线性系统，n 阶运动方程式的系统可以分离为以模态位移向量 {x} 表示的 n 个单自由度方程式：
（方程式 4）
替换（方程式 4）中的向量 {u} 并将它预乘以 [Φ]T（方程式 1）将形成：
（方程式 5）
正常模式满足正交状态属性，模态矩阵 [Φ] 经过正规化，可以满足以下方程式：
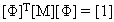（方程式 6）
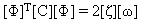（方程式 7）和
（方程式 8）。
通过替换（方程式 6）到（方程式 8），（方程式 5）会成为一组 n 阶独立 SDOF 二阶微分方程式：
(i =1, ..., n)（方程式 9）
（方程式 9）通过诸如威尔逊-塞塔和纽马克的逐步积分方法解出。
积分是在时间域中执行的，在时间域中，上一步的结果会用来预测下一步的结果。
系统的位移向量 (u) 从（方程式 4）派生而来。