Pomocí harmonické analýzy lze počítat špičkovou odezvu systému v klidovém stavu v důsledku harmonických zatížení nebo základových buzení.
Harmonické zatížení P je vyjádřeno jako P = A sin (ωt + φ), kde: A je amplituda, ω je frekvence, t je čas a φ je fázový úhel. Vzorová harmonická zatížení o různých frekvencích w v závislosti na čase jsou zobrazena níže:

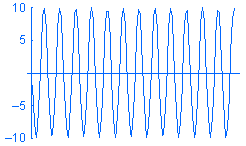
Ačkoli lze vytvořit studii modálního časového průběhu a určovat zatížení jako funkce času, přechodové změny v závislosti na čase nemusejí být vždy požadovány. V takových případech lze šetřit čas a zdroje vyřešením špičkové odezvy ustáleného stavu v požadovaném rozsahu provozních frekvencí pomocí harmonické analýzy.
Například motor upevněný na zkušební stolici přenáší harmonické zatížení na systém podpěr prostřednictvím šroubů. Podpůrný systém lze modelovat a určit harmonickou studii k vyhodnocení špičkových posunů, napětí atd. v ustáleném stavu pro rozsah provozních frekvencí daného motoru. Motor můžete přibližně zpracovat pomocí rozptýlené hmoty.

Po spuštění studie lze zobrazit špičkové amplitudy parametrů reakce (napětí, posuny, zrychlení a rychlosti) a také obrázky reakce fázových úhlů parametrů reakce v celém rozsahu provozních frekvencí.
Když se spustí harmonická studie, obrázek obrysů parametru reakce zobrazí absolutní špičkové hodnoty sinusoidní časové historie reakce v příslušném frekvenčním kroku. Přechodová sinusoidní část parametru reakce a jeho fázový úhel se v obrázku nezobrazují. V případě kroku pracovní frekvence, který se blíží přirozené frekvenci modelu, je obrázek tvaru režimu realističtější reprezentací deformovaného tvaru než obrázek obrysů posunutí na příslušné frekvenci.
Můžete vytvořit obrázek reakce pro parametr reakce (posunutí, napětí, rychlost nebo zrychlení) napříč všemi frekvenčními kroky řešení.
Možnosti modálního, Rayleighova a složeného modálního tlumení jsou pro tento typ analýzy k dispozici.