Die symmetrische Dämpfungsmatrix n x n [C] wird als lineare Kombination von Masse- [M] und Steifigkeitsmatrizen [K] formuliert:
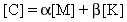(Gleichung 1)
-
Alpha-Koeffizient: Definiert den masse-proportionalen Koeffizienten α.
-
Beta-Koeffizient: Definiert den steifigkeits-proportionalen Koeffizienten β.
Der in (Gleichung 1) beschriebene Dämpfungstyp wird als Rayleigh- oder proportionale Dämpfung bezeichnet.
Diese Form von [C] ist in Bezug auf die Eigenvektoren des Systems orthogonal.
Durch Anwendung der modalen Koordinatenumwandlung wird die modale Dämpfungsmatrix [c] diagonal:
(Gleichung 2)
Rayleigh-Dämpfung kann für lineare und nicht lineare dynamische Studien definiert werden.
Beziehung zwischen Rayleigh-Koeffizienten und modalem Dämpfungsverhältnis
Die modale Dämpfungsmatrix [c] ist angegeben durch:
(Gleichung 3)
Der Koeffizient der viskosen Dämpfung ci für die ite-Schwingung errechnet sich wie folgt:
(Gleichung 4)
und das viskose Dämpfungsverhältnis ζi wird ausgedrückt durch
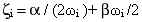(Gleichung 5)
Wenn die Dämpfungsverhältnisse für die ite- und jte-Schwingungen ζi und ζj sind, errechnen sich die Rayleigh-Koeffizienten α und β aus der Lösung der beiden algebraischen Gleichungen:
(Gleichung 6)
Wenn beide Modi das gleiche Dämpfungsverhältnis (ζi = ζj = ζ) aufweisen, werden die Werte von α und β ausgedrückt durch:
(Gleichung 7) 
(Gleichung 8)
Das viskose Dämpfungsverhältnis ζ für alle anderen Schwingungen verändert sich in Abhängigkeit von der Frequenz, wie in der Abbildung dargestellt:
