Il sistema di equazioni del movimento di un sistema lineare di n gradi di mobilità ingrandito da una forza variante è:
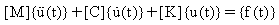 (Equazione 1)
(Equazione 1)
Usando la trasformazione delle coordinate, il gruppo di n equazioni simultanee riduce ad n equazioni indipendenti (ogni equazione può essere risolta indipendentemente):
 per r = 1, 2, ...., n (Equazione 2)
per r = 1, 2, ...., n (Equazione 2)
dove xr(t) sono le coordinate modali correlate alle coordinate nodali ur(t) per:
 (Equazione 3).
(Equazione 3).
Il vettore dei carichi modali {m(t)} è dato da:
 (Equazione 4).
(Equazione 4).
Assumendo che le eccitazioni sono espresse secondo le relative funzioni di densità spettrali (psd), la soluzione può essere formulata nel dominio della frequenza. Se la matrice psd di eccitazione è data da [Sf(ω)], la matrice psd della forza modale è definita come:
 (Equazione 5).
(Equazione 5).
Il valore psd del responso di spostamento modale [Sx(ω)] si ottiene da:
 (Equazione 6),
(Equazione 6),
dove [H(ω)] è la matrice della funzione di trasferimento modale e [H*(ω)] il coniugato complesso. Per le modalità normali, la matrice della funzione di trasferimento è diagonale con elementi diagonali Hr(ω)
 (Equazione 7) e
(Equazione 7) e
 (Equazione 8).
(Equazione 8).
Il psd di responso dello spostamento [Su(ω)] è quindi derivato da (Equazione 3).
 (Equazione 9).
(Equazione 9).
Il psd della velocità e dei responsi di accelerazione sono espressi da:
 (Equazione 10) e
(Equazione 10) e
 (Equazione 11).
(Equazione 11).
Il psd della velocità modale e dell'accelerazione sono correlati al psd di spostamento modale in questo modo:
 (Equazione 12) e
(Equazione 12) e 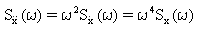 (Equazione 13)
(Equazione 13)
Equazione 10 e Equazione 11 possono essere riscritte in questo modo:
 (Equazione 14) e
(Equazione 14) e (Equazione 15).
(Equazione 15).
I responsi di autocorrelazione modale con ritardo zero (τ=0) in termini di psd del responso modale sono calcolati dagli integrali:
 (Equazione 16)
(Equazione 16)
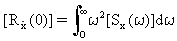 (Equazione 17)
(Equazione 17)
 (Equazione 18).
(Equazione 18).
Dalle equazioni sopra riportate, i responsi quadrati sono determinati dai termini diagonali delle matrici:
 (Equazione 19),
(Equazione 19),
 (Equazione 20),
(Equazione 20),
 (Equazione 21).
(Equazione 21).
Responso quadrato principale della sollecitazione
Le sollecitazioni dell'elemento {σ} sono determinate dagli spostamenti nodali {u} per:
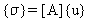 (Equazione 22) o in termini degli spostamenti modali {x} per:
(Equazione 22) o in termini degli spostamenti modali {x} per:
 (Equazione 23), dove [Φ] è la matrice dei vettori eigen.
(Equazione 23), dove [Φ] è la matrice dei vettori eigen.
La matrice di correlazione della sollecitazione [Rσ] è data da:
 (Equazione 24).
(Equazione 24).