物体内部の内力は、ある点から別の点へと変化します。荷重は、任意の小さな内部平面領域の一方の側にある物体の一部によって、その領域を横切って反対側の部分に及ぼされます。応力は、これらの内力の強度(単位面積あたりの力)を意味します。
応力(Stress)
連続体では、ある点の応力を次のように可視化した形で理解することができます。
- ある点を通って物体を切断する面を考えてください。
- その面上の点の近傍で無限に小さな領域 ΔA を想定してください。
- ある方向に ΔA を通って伝わる力の強さは ΔF であるとします。
- その方向に対する応力は ΔA が 0 に近づくに従って ΔF/ΔA となります。
上記は点における応力、または、トラクションベクトルを定義します。トラクションベクトルは点における応力の状態をユニークに定義しません。それは選択された任意の平面によって変化します。応力テンソル、たとえば、実際の応力テンソルは σ = n.T (マトリックス乗算)として定義します。n は平面に関連する垂直ベクトルで、T は応力、またはトラクション ベクトルで、ユニークに応力を定義します。
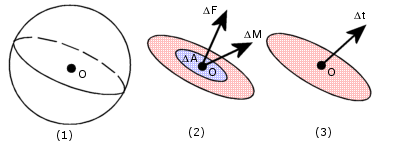
図 (1): O 点を通って物体を切断する面を考え、二つの部品に分解する。
図 (2): 合成力またはモーメントは、平面の中で O 点に関する領域 ΔA 上にベクトルができます。
図 (3): O 点における応力ベクトルはこのようになります。
ひずみ(Strain)
ひずみは長さの変化量 δL と基本の長さ L の比率です。ひずみは無次元量で表されます。
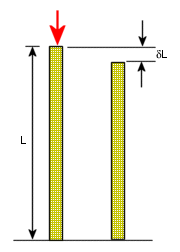
ひずみ = δL/L
計算手順(Sequence of Calculations)
メッシュ分割されたモデルで、変位を拘束し、荷重が与えられると、線形静解析プログラムは次のように計算します:
- プログラムは、有限要素の釣り合い方程式から線形連立一次方程式を作り上げ、それを解いて、各節点での変位を求めます。
- その後、プログラムはひずみ成分を計算するために変位結果を使用します。
- プログラムは応力を計算するためにひずみ結果や応力とひずみの関係を使用します。

応力の計算
最初に、応力は要素内にあるガウス点または求積点と呼ばれる特別な点で計算されます。これらの点は、最適な結果をもたらすよう選択されます。プログラムは、このガウス点の結果を外挿して、各要素の節点での応力を計算します。
計算が無事終了すると、各要素の節点での応力はデータベース内で使用可能になります。二つあるいはそれ以上の要素で共有されている節点では、一つ以上の結果が存在することになります。しかも、これらは必ずしも同じ値にはなっていません。それは、有限要素法が近似計算手法だからです。たとえば、一つの節点が三つの要素に共有されている場合、僅かばかり異なる三つの応力値をその節点が持つことになります。
応力結果を表示するときに、要素応力または節点応力を求めることができます。要素応力の場合は、すべての関連要素の寄与成分を平均して求めます。節点応力の場合は、その節点を共有するすべての要素の寄与成分を平均して求めます。