점성 효과로 인해 역학적 에너지를 분산하는 특성이 있는 탄성 재질을 점탄성 재질이라고 할 수 있습니다.
다축 응력 상태일 경우 구성 방정식은 다음과 같습니다.

위치: e(bar) 및 φ는 편차 및 볼륨 변형이고, G(t - τ) 및 K(t - τ)는 전단 및 벌크 이완 함수입니다.
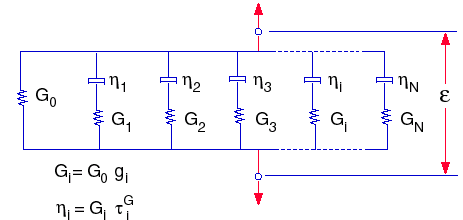
이완 함수는 기계적 모델로 표현할 수 있습니다. 이 모델을 대개 일반 맥스웰 모델이라고 하며 다음과 같이 표현됩니다.

위치: G0 = E / 2(1+ ν), 초기 전단 계수(t=0)
및 K0= E / 3(1 -2ν), 초기 벌크 계수(t=0)
gi, ki, τi
G 및 τi
K는 i번째 전단과 벌크 계수 및 해당하는 시간입니다.
재질의 동작에서 온도의 효과는 시간 온도 대응 원칙을 통해 도입됩니다. 이 원칙의 연산 식은 다음과 같습니다.

여기서 γt는 감소된 시간이고 γ는 전환 함수입니다. WLF(Williams-Landel-Ferry) 수식을 사용하여 함수의 대략적인 값을 구합니다.
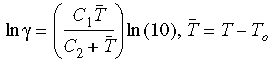
여기서, T0은 참조 온도로서, 대개 유리 전이 온도로 사용되며 C1과 C2는 재질 의존 상수입니다.
| 파라미터 |
재질 속성 |
|---|
| 선형 탄성 파라미터 |
X 방향의 탄성계수
|
|
xy 평면의 포아송비
|
|
XY 평면의 전단계수
|
| 이완 함수 파라미터 |
전단 이완 계수(1~8) (일반 맥스웰 모델 수식에서 g1, g2, ...,g8를 나타냄)
|
|
시간 값(전단 이완 계수 1 - 8)(일반 맥스웰 모델 수식에서 τ1
g, τ2
g,..., τ8
g 등을 나타냄) |
|
벌크 이완 계수(1~8) |
|
시간 값(벌크 이완 계수 1 - 8)(일반 맥스웰 모델 수식에서 τ1
g, τ2
g,..., τ8
g 등을 나타냄) |
| WLF 수식 파라미터
|
유리 전이 온도
(WLF 수식에서 T0을 나타냄)
|
|
First Constant for Williams-Landel-Ferry equation
(WLF 수식에서 C1을 나타냄)
|
|
Second Constant for Williams-Landel-Ferry equation
(WLF 수식에서 C2를 나타냄)
|
테이블 및 곡선 탭 아래 전단 또는 벌크 이완 곡선을 정의할 때, 곡선의 첫 점은 t1일 때 G1 또는 K1 계수입니다. 시간 t = 0에서, 프로그램이 자동으로 탄성 계수와 포아송비에서 G0 또는 K0을 계산합니다.
점탄성 재질 모델을 시험 품질 및 고품질 솔리드와 쉘 요소와 함께 사용할 수 있습니다.
점탄성 재질 모델을 사용할 때 비선형 해석에서 시간은 실제값입니다.