W przeciwieństwie do materiału izotropowego, materiał ortotropowy posiada preferowane kierunki wytrzymałości, które są do siebie wzajemnie prostopadłe. Właściwości wzdłuż tych kierunków (znanych również jako kierunki główne) są ekstremalnymi wartościami współczynników sprężystości.
Macierz [D] dla materiału ortotropowego zawiera dziewięć niezależnych właściwości sprężystości. Dodatkowo występują trzy właściwości wynikające z rozszerzalności termicznej.
Dwuwymiarowe ortotropowe relacje rozciągania
Ortotropowe relacje rozciągania w dwóch wymiarach z uwzględnieniem efektów termicznych można zapisać następująco:
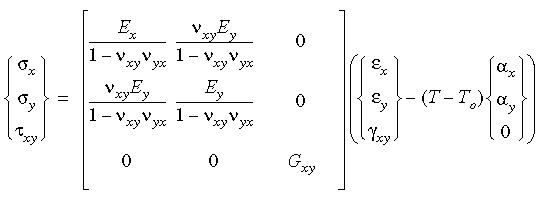
Należy zauważyć, że w celu zapewnienia symetrii macierzy współczynników sprężystości wzdłużnej νxy Ey = νyx Ex.
Spełnienie powyższego warunku symetrii jest konieczne podczas wprowadzania wartości numerycznych współczynnika sprężystości wzdłużnej oraz współczynnika Poissona.
Ponadto, jeżeli wartość numeryczna współczynnika ścinania nie zostanie wprowadzona, to program obliczy go w poniższy sposób:
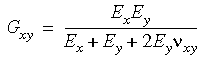
Warunki symetrii ortotropowej w trzech wymiarach wymagają:
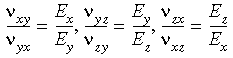
Dlatego też podczas wprowadzania właściwości materiału ortotropowego w trzech wymiarach, konieczne jest zapewnienie spełnienia powyższych warunków symetrii.
W przypadku, gdy użytkownik wprowadzi wartości liczbowe dla współczynników ścinania (Gxy, Gyz i Gxz), zostaną one użyte przez program (nawet jeśli nie będą spełniać warunków symetrii ortotropowej).
Zauważmy, że jeżeli wartości numeryczne współczynników ścinania nie zostaną wprowadzone, to program obliczy je z wykorzystaniem poniższych zależności:

Jeżeli Ex = Ey = Ez, program oblicza współczynnik ścinania wewnętrznie, nawet gdy jest on jawnie zdefiniowany.
Program przyjmuje wartości 0.0 dla współczynników Poissona, które nie zostały jawnie zdefiniowane.