A avaliação de danos de fadiga para componentes que operam em um ambiente de vibração aleatória é estimada no domínio da frequência com base nas propriedades estatísticas da função de densidade espectral de potência (PSD) de tensão de resposta.
Quando as estruturas ou componentes mecânicos são submetidos a uma forma aleatória de carga, como uma turbina eólica sofrendo carga do vento, uma estrutura offshore sofrendo carda de uma onda ou um motor de carro sendo operado em diferentes perfis de pavimentação de estrada, as estimativas de vida de fadiga são executadas no domínio da frequência.
O termo fadiga de vibração (ou fadiga com base na frequência) refere-se à estimativa da vida de fadiga onde a carga e resposta (históricos de tensão e deformação) são processos aleatórios, e, portanto, são melhores descritos usando medidas estatísticas como densidade espectral de potência (funções de PSD).
As características estatísticas da PSD de tensão de resposta podem ser obtidas através dos momentos da função de PSD.
| Características estatísticas de PSD |
Equação |
|---|
| O no momento espectral da PSD da tensão S(f) na frequência f (em unidades de Hz). |
 (Eq.1) (Eq.1)
|
| Valor da raiz quadrada média para um processo σ Gaussiano estacionário contínuo . |
 (Eq.2) (Eq.2)
|
| Número médio de cruzamentos de zero ascendente E[0] para uma amostra típica de 1 segundo. |
 (Eq.3) (Eq.3)
|
| Número médio de picos E[p] para uma amostra típica de 1 segundo. |
 (Eq.4) (Eq.4)
|
| O fator de irregularidade y varia entre 0 e 1. Ele se aproxima de 1 à medida que o sinal de tensão se aproxima de um processo de banda estreita (por uma onda de seno y=1). Ele se aproxima de 0 à medida que o sinal de tensão se aproxima de um processo de ruído branco. |
 (Eq.5) (Eq.5)
ou
 (Eq.6) (Eq.6)
|
As propriedades da fadiga de material normalmente são obtidas de uma curva S-N, que define o relacionamento entre o alcance de tensão, S (esta é a variação de tensão da tensão cíclica máxima na tensão até a tensão cíclica mínima na compressão) em relação à média ciclos para falha, N.
Para a maioria dos problemas de fadiga de ciclos elevada (N >= 104 ), a curva S-N pode ser expressa de forma simplificada:
 (Eq.7)
(Eq.7)
onde B e m são propriedades do material que variam com as condições de carga e do ambiente e são determinadas por experimentos de testes de fadiga.
Os danos acumulados E [AD] devido à fadiga por carga aleatória são baseados na regra de Palmgren-Miner e são expressos como:
 (Eq.8)
(Eq.8)
onde n(S) é o número de ciclos aplicados ao nível de alcance de tensão S, p(S) é a função de densidade de probabilidade do alcance de tensão. Substituindo a equação simplificada da curva S-N na equação acima, é obtida uma equação geral de dano por fadiga de resposta de tensão aleatória:
 (Eq.9), onde T é o tempo de em segundos da carga aleatória.
(Eq.9), onde T é o tempo de em segundos da carga aleatória.
Estão disponíveis três métodos de estimativa de dano por fadiga baseados na Eq.9: método de três bandas de Steinberg, método de banda estreita e método de Wirshing. Cada método usa uma definição diferente para a função de densidade de probabilidade p(S).
Método de banda estreita
No método de banda estreita, a função de densidade de probabilidade de picos para um sinal de banda estreita tende para uma distribuição Rayleigh (Bendat J. S., Probability Functions for Random Responses. Relatório da NASA em contato NASA-5-4590, 1964).
 (Eq.10)
(Eq.10)
Substituindo a (Eq.10) em (Eq.9) e integrando resultados à seguinte expressão para estimativa do dano por fadiga.
 (Eq.11), onde Γ( .) é a função Gama.
(Eq.11), onde Γ( .) é a função Gama.
Método de Wirsching
O método de Wirsching (Wirshing, P. H. , Paez, T. L. , e Ortiz K., Random Vibration, John Wiley & Sons Inc., Nova York, 1995) modifica o método de banda estreita com um fator de correção empírica para levar em consideração um processo de banda larga.
 (Eq. 12)
(Eq. 12)
 , (Eq. 13)
, (Eq. 13)
ζw é um fator empírico derivado de simulações Monte Carlo que incluem uma variedade de funções de densidade espectral.
αw e bw são os parâmetros mais adequados considerando:
 (Eq. 14)
(Eq. 14)
Método da três bandas de Steinberg
A suposição do método de Steinberg é que a função de densidade de probabilidade da resposta de tensão aleatória segue uma distribuição gaussiana, e, portanto, os valores esperados das amplitudes de resposta de tensão são limitados por certos níveis de probabilidade:
- 68,27 % de chance de a amplitude dos ciclos de tensão não excederem o alcance de 2 vezes a raiz quadrada média do sinal de resposta de tensão.
- 27,1 % de chance de a amplitude dos ciclos de tensão não excederem o alcance de 4 vezes a raiz quadrada média do sinal de resposta de tensão.
- 4,3% de chance de os ciclos de tensão não excederem o alcance de 6 vezes a raiz quadrada média do sinal de resposta de tensão.
Não há ciclos de tensão ocorrendo com alcances maiores que 6 vezes a raiz quadrada média.
O dano por fadiga esperado é obtido por:
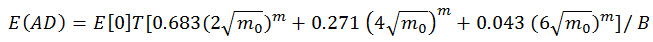 (Eq.15)
(Eq.15)
Na simulação, as funções de tensão da PSD são os resultados do estudo de vibração dinâmico-aleatória no qual o estudo de fadiga é baseado. O componente de tensão de vonMises é considerado para o cálculo dos danos esperados devido à fadiga para todos os três métodos.