Los análisis armónicos evalúan la respuesta de estado estable pico de un sistema a cargas armónicas.
En cada paso de solución, todas las cargas aplicadas y excitaciones de la base tienen la misma frecuencia. Las curvas de frecuencia asociadas definen las magnitudes.
Supongamos un vector de fuerza nodal armónica {P} definido como:
 (Ecuación 1) o
(Ecuación 1) o  (Ecuación 2),
(Ecuación 2),
donde:
Pk es la magnitud de la fuerza en la dirección del grado de libertad kth
ω es la frecuencia de excitación e
γk es el ángulo de fase de la fuerza.
Para sistemas lineales, las ecuaciones de movimiento del sistema están desacopladas en n ecuaciones modales:
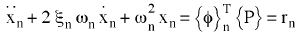 (Ecuación 3).
(Ecuación 3).
Al sustituir el vector de fuerza {P} por (Ecuación 3) da como resultado:
 (Ecuación 4), donde
(Ecuación 4), donde
 (Ecuación 5)
(Ecuación 5)
La solución de estado estable para (Ecuación 4) es:
 (Ecuación 6).
(Ecuación 6).
La pieza real para (Ecuación 6) es:
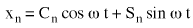 (Ecuación 7) donde
(Ecuación 7) donde
 (Ecuación 8) y
(Ecuación 8) y
 (Ecuación 9).
(Ecuación 9).
El vector de desplazamiento viene dado por:
 (Ecuación 10) o
(Ecuación 10) o
 (Ecuación 11)
(Ecuación 11)
La magnitud de desplazamiento uk y el ángulo de fase correspondiente θkpara el grado de libertad kth son:
 (Ecuación 12)
(Ecuación 12)
Las respuestas de velocidad y aceleración se derivan de las derivadas de (Ecuación 11). Sus amplitudes son:
 (Ecuación 13)
(Ecuación 13)
Los ángulos de fase de las velocidades y aceleraciones están 90º y 180º fuera de la fase con respecto a los ángulos de fase de desplazamiento.