La opción de la simplificación 2D modela el problema mediante una suposición de deformación unitaria plana. El desplazamiento en una de las direcciones es insignificante con respecto a las otras dos. La condición de deformación unitaria plana es válida si:
- Una de las cotas es mucho mayor que las otras dos.
- Las fuerzas en plano no varían a lo largo de la cota más grande.
- Las fuerzas que actúan de forma normal al plano de sección son insignificantes.
La figura muestra un sólido grueso bajo los efectos de cargas uniformes. La cota de Y es mucho mayor que las cotas de X y Z. Para modelar el problema, cree un plano de sección que sea paralelo al plano XZ, especifique el espesor y aplique cargas y sujeciones a las aristas.
Puede crear varios sólidos 2D mediante un plano de sección y definir condiciones de contacto entre ellos.
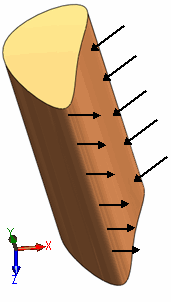
Las siguientes simplificaciones son válidas para los resultados de la simulación.
| Desplazamiento, carga y temperatura |
El desplazamiento y la temperatura no varían a lo largo del espesor. Para el sólido grueso:
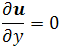 donde u es el vector de desplazamiento. Además, uy = 0, donde u es el vector de desplazamiento. Además, uy = 0,
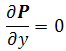 donde P es el vector de carga. Además, Py=0, donde P es el vector de carga. Además, Py=0,
y
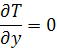 donde T es la temperatura. donde T es la temperatura.
|
| Tensión |
Todos los componentes de tensión son distintos de cero. Sin embargo, los componentes de tensión fuera del plano existen como consecuencia del efecto del coeficiente de Poisson y no tienen una función importante en el análisis. |
| Deformación unitaria |
Los componentes de tensión fuera del plano son nulos. Sólo existen los componentes de tensión en el plano. Para el sólido grueso:
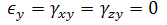 donde ε representa la tensión normal y γ representa la deformación unitaria cortante. donde ε representa la tensión normal y γ representa la deformación unitaria cortante.
|