Different control techniques have been devised to perform nonlinear analysis. These techniques can be classified as:
Incremental Load Control Method
In this strategy, the loads applied to the system are used as the prescribed variables. Each state (point) on the equilibrium path is determined by the intersection of a surface (F = constant) with the path to determine the deformation parameters.
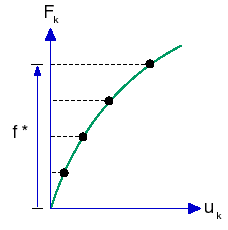
In adapting this technique for finite element analysis, the loads (base motions, prescribed displacements, thermal, gravity, etc.) are incrementally applied as specified by the associated “time” curves.
Incremental Displacement Control Method
In this technique, a point on the equilibrium path is determined by the intersection of a surface defined by a constant deformation parameter (U = constant) with the solution curve as shown in the figure below.

To incorporate this technique in finite element analysis, the pattern of the applied loads is proportionally incremented (using a single load multiplier) to achieve equilibrium under the control of a specified degree of freedom. The controlled DOF, specified by selecting a vertex or a reference point, is incremented through the use of a “time” curve.
Incremental Arc-Length Control Method
In this strategy, a special parameter is prescribed by means of a constraint (auxiliary) equation which is added to the set of equations governing the equilibrium of the system. In the geometric sense, the control parameter can be viewed as an “arc length” of the equilibrium path as shown in the figure below.
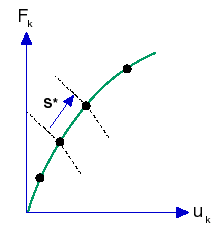
To use this technique in finite element analysis, the pattern of the applied loads is proportionally incremented (using a single load multiplier) to achieve equilibrium under the control of a specified length (arc-length) of the equilibrium path. The arc-length will be automatically calculated by the program. No “time” curve is required.
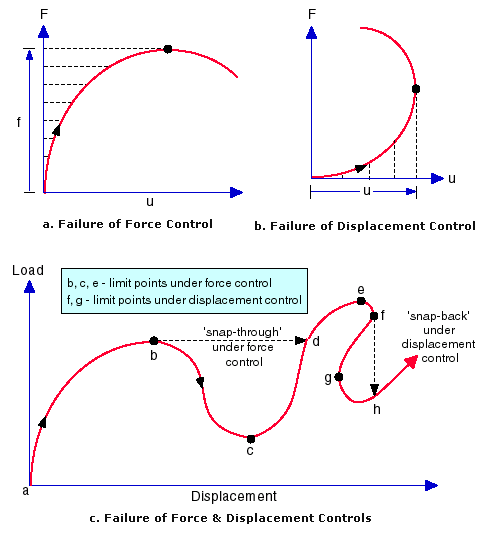
Both force control and displacement control will breakdown in the neighborhood of turning points (known as snap-through for force control and snap-back for displacement control) as in the following figure. These difficulties usually are encountered in buckling analysis of frames, rings, and shells. Arc-Length control will successfully overcome these difficulties.