時変荷重によって動く線形 n-自由度系システムの運動方程式は次のようになります:
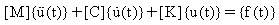(関係式 1)
ここで、
[M] = n x n 対称慣性マトリックス
[C] = n x n 対称減衰マトリックス
[C] = n x n 対称剛性マトリックス
{f(t)} = n-次力ベクトル
{u}、
、
はそれぞれ変異、速度、加速度（n 次ベクトル）です。
(関係式 1) は一定係数を持つ n 連立常微分方程式です。運動方程式は質量、剛性、減衰を介して結合されています。結合は、運動方程式を数学的に記述するために使用した座標系に依存します。
モーダル解析の基本的概念は、(関係式 1)の結合されたシステムをモーダル行列 [Φ] を変換行列として使用し、一組の独立した方程式に変換することにあります。[Φ] にはノーマル モード {f}i が i = 1, ....,n のために含まれ、次のように配列されます:
(関係式 2)
ノーマルモードとシステムの固有値は固有値問題の解から導かれます:
(関係式 3)
ここで [ω2] は固有振動数の二乗の対角行列です。
線形システムでは、n 運動方程式システムをモーダル変位ベクトル {x} を使用して結合解除し n-1自由度方程式にできます:
(関係式 4)
ベクトル {u}（関係式 4）を置き換え、[Φ]T（関係式 1）で事前乗算すると次のようになります:
(関係式 5)
ノーマル モードが直交性プロパティを満たし、モーダル行列 [Φ] が正常化され次の式を満たします:
(関係式 6)
(関係式 7) と
(関係式 8)
(関係式.6--8) を置き換えると、(関係式 5) が n 独立 SDOF 二次の微分方程式になります:
for i =1, ..., n（関係式 9）
（関係式 9）は Wilson-Theta や Newmark などの段階的な積分法で解くことができます。
積分法は時間領域内（最後のステップの結果が次のステップの予測に使用されます）で実行されます。
システムの変位ベクトル (u) は (関係式 4) から導かれます。