A função de densidade da energia de deformação de Ogden, definida como
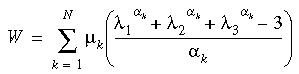
onde: λi são os trechos principais, αi, μi são constantes do material e N é o número de termos na função, que é considerada uma das funções que melhor descreve a ampla faixa de deformação de materiais semelhantes à borracha.
A função de penalização usada na fórmula do modelo de Ogden assume a forma usada no modelo de Mooney-Rivlin. A função de energia de deformação de fato usada é um tipo modificado da função de Ogden.
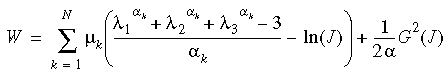
em que J é o raio do volume deformado ao volume não deformado, N é o número de termos na função, G(J) = J2-1, e
 onde ν é o Coeficiente de Poisson.
onde ν é o Coeficiente de Poisson.
Os modelos de 3 termos (Ogden modificado) são amplamente usados. Modelos para até 4 termos (N = 4) estão disponíveis no programa.
Além das constantes de materiais mencionadas acima, o coeficiente de Poisson também é requerido. Para a maioria dos casos, resultados satisfatórios podem ser obtidos atribuindo-se coeficientes de Poisson de 0,49 a 0,499. Além disso, o aumento do coeficiente de Poisson não afeta significativamente os resultados numéricos, a menos que uma deformação volumétrica considerável seja envolvida.
Quando o coeficiente de Poisson está extremamente próxima de 0,5, ele pode causar o término da solução devido aos termos negativos diagonais na matriz de rigidez ou devido à falta de convergência.
As propriedades de material para o modelo Ogden são inseridas na caixa de diálogo
Material. As quantidades exigidas são:
- Coeficientes de materiais da primeira à quarta potência (αi)
- Constantes de materiais da primeira à quarta potência (μi) (depende do número de constantes).
- Coeficiente de Poisson