La evaluación del daño de la fatiga para los componentes que funcionan en un entorno de vibración aleatoria se calcula en el dominio de frecuencia en función de las propiedades estadísticas de la función de densidad espectral de potencia (PSD) de la tensión de respuesta.
Cuando las estructuras o los componentes mecánicos están sometidos a una carga de tipo aleatorio, como una turbina de viento bajo una carga de viento, una estructura terral bajo una carga de olas o un motor de automóvil que funcione en distintos perfiles de superficie de carretera, los cálculos del ciclo de fatiga se realizan en el dominio de frecuencia.
El término fatiga de vibración (o fatiga basada en frecuencia) hace referencia al cálculo del ciclo de fatiga donde la carga y respuesta (historiales de tensión y deformación unitaria) son procesos aleatorios y, por lo tanto, se describen mejor mediante medidas estadísticas como la densidad espectral de potencia (funciones PSD).
Las características estadísticas de la densidad espectral de potencia de la tensión de respuesta pueden obtenerse en los momentos de la función PSD.
| Características estadísticas de PSD |
Ecuación |
| El momento espectral nth de la densidad espectral de potencia de tensión S(f) a una frecuencia f (en unidades de Hz). |
 (Ecuación 1) (Ecuación 1)
|
| Valor de media cuadrática para un proceso gaussiano estacionario continuo σ. |
 (Ecuación 2) (Ecuación 2)
|
| Promedio de cruces cero hacia arriba E[0] para una muestra de 1 segundo típica. |
 (Ecuación 3) (Ecuación 3)
|
| Promedio de picos E[p] para una muestra de 1 segundo típica. |
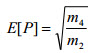 (Ecuación 4) (Ecuación 4)
|
| El factor de irregularidad γ varía entre 0 y 1. Se aproxima a 1 a medida que la señal de tensión se aproxima a un proceso de banda estrecha (para una onda de seno γ =1). Converge en 0,745 a medida que la señal de tensión se aproxima a un proceso de ruido blanco. |
 (Ecuación 5) (Ecuación 5)
o
 (Ecuación 6) (Ecuación 6)
|
Las propiedades de fatiga de materiales se obtienen generalmente de una curva S-N, que define la relación entre el intervalo de tensión, S (la variación de tensión desde la tensión cíclica máxima en tensión hasta la tensión cíclica mínima en compresión) frente a la media de ciclos hasta el fallo, N.
Para la mayoría de los problemas de fatiga de ciclo alto (N >= 104), la curva S-N se puede expresar de forma simplificada:
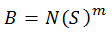 (Ecuación 7)
(Ecuación 7)
donde B y m son las propiedades de materiales que varían con la carga y las condiciones ambientales y están determinadas por los experimentos de pruebas de fatiga.
El daño acumulado E[AD] debido a la fatiga derivada de la carga aleatoria se basa en la regla de Palmgren-Miner y se expresa como:
 (Ecuación 8)
(Ecuación 8)
donde n(S) es el número de ciclos que se aplican en el nivel S del intervalo de tensión, p(S) es la función de densidad de probabilidad del intervalo de tensión. Al sustituir la ecuación de la curva S-N simplificada en la ecuación anterior, se obtiene una ecuación general de daño de fatiga a partir de la respuesta de tensión de:
 (Ecuación 9), donde T es la duración en segundos de la carga aleatoria.
(Ecuación 9), donde T es la duración en segundos de la carga aleatoria.
Hay disponibles tres métodos para la estimación del daño de fatiga basado en la ecuación 9: Método Steinberg de tres bandas, método de banda estrecha y método Wirsching. Cada método utiliza una definición diferente para la función de densidad de probabilidad p(S).
Método de banda estrecha
En el método de banda estrecha, la función de densidad de probabilidad de picos para una señal de banda estrecha tiende a una distribución Rayleigh (según el informe sobre funciones de probabilidad para respuestas aleatorias de Bendat J. S., Probability Functions for Random Responses. NASA report on Contract NASA-5-4590, 1964).
 (Ecuación 10)
(Ecuación 10)
Sustituir (Ecuación 10) en (Ecuación 9) e integrar los resultados en la siguiente expresión para la estimación del daño de fatiga.
 (Ecuación 11), donde Γ(.) es la función Gamma.
(Ecuación 11), donde Γ(.) es la función Gamma.
Método de Wirsching
El método de Wirsching (Wirshing, P.H., Paez, T.L. y Ortiz K., Vibración aleatoria, John Wiley & Sons Inc., Nueva York, 1995) modifica el método de banda estrecha con un factor de corrección empírico para tener en cuenta un proceso de banda ancha.
 (Ecuación 12)
(Ecuación 12)
 , (Ecuación 13)
, (Ecuación 13)
ζw es un factor empírico derivado de las simulaciones de Monte Carlo que incluyen una variedad de funciones de densidad espectral.
αw y bw son los mejores parámetros de ajuste que se obtienen de:
 (Ecuación 14)
(Ecuación 14)
Método Steinberg de tres bandas
La suposición del método de Steinberg se basa en que la función de densidad de probabilidad de la respuesta de tensión aleatoria sigue una distribución gaussiana y, por lo tanto, los valores esperados de las amplitudes de respuesta de tensión están vinculados por determinados niveles de probabilidad:
-
Hay una probabilidad del 68,27 % de que la amplitud de los ciclos de tensión no exceda el intervalo de 2 veces la media cuadrática de la señal de respuesta de tensión.
- Hay una probabilidad del 27,1 % de que la amplitud de los ciclos de tensión no exceda el intervalo de 4 veces la media cuadrática de la señal de respuesta de tensión.
- Una probabilidad del 4,3 % de que los ciclos de tensión no excedan el intervalo de 6 veces la media cuadrática de la señal de respuesta de tensión.
No hay ciclos de tensión que se produzcan con intervalos superiores al intervalo de 6 veces la media cuadrática.
El daño de fatiga esperado se genera por:
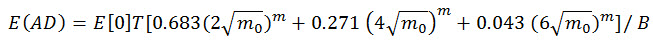 (Ecuación 15)
(Ecuación 15)
En la simulación, las funciones PSD de tensión son el resultado del estudio de vibración aleatoria dinámica en el que se basa el estudio de fatiga. El componente de tensión de vonMises se tiene en cuenta para el cálculo del daño esperado debido a la fatiga para los tres métodos.