Das System von Bewegungsgleichungen eines linearen n-Freiheitsgrad-Systems, erregt durch eine zeitvariierende Kraft ist:
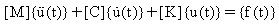(Gleichung 1)
wobei:
[M] = n x n symmetrische Trägheitsmatrix
[C] = n x n symmetrische Dämpfungsmatrix
[K] = n x n symmetrische Steifigkeitsmatrix
{f(t)} = n-dimensionaler Kraftvektor
{u},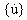 
und 
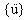sind die n-dimensionalen Verschiebungs-, Geschwindigkeits- und Beschleunigungsvektoren.
(Gleichung 1) ist ein System von n gleichzeitigen gewöhnlichen Differentialgleichungen mit konstanten Koeffizienten. Die Bewegungsgleichungen sind gekoppelt durch die Masse-, Steifigkeits- und Dämpfungswerte. Die Kopplung hängt vom Koordinatensystem ab, das für die mathematische Beschreibung der Bewegungsgleichungen verwendet wird.
Der Grundgedanke hinter einer Modalanalyse ist die Transformation des gekoppelten Systems von (Gleichung 1) in eine Reihe unabhängiger Gleichungen durch die Verwendung der Modalmatrix [Φ] als Transformationsmatrix. [Φ] enthält die Normalschwingungen {f}i für i = 1, ....,n festgehalten als:
(Gleichung 2)
Die Normalschwingungen und Eigenwerte des Systems sind abgeleitet von der Lösung des Eigenwert-Problems:
(Gleichung 3)
wobei [ω2] eine Diagonalmatrix der Eigenfrequenzen zum Quadrat sind.
In linearen Systemen kann das System von n Bewegungsgleichungen in n Einzelfreiheitsgrad-Gleichungen des modalen Verschiebungsvektors {x} entkoppelt werden:
(Gleichung 4)
Ein Ersetzen des Vektors {u} von (Gl.4) und Vormultiplizieren mit [Φ]T (Gleichung 1) ergibt:
(Gleichung 5)
Die Normalschwingungen erfüllen die Orthogonalitätseigenschaft, und die Modalmatrix [Φ] wird normalisiert, um die folgenden Gleichungen zu erfüllen:
(Gleichung 6)
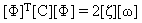(Gleichung 7) und
(Gleichung 8).
Durch Ersetzen (Gleichungen 6--8) wird die (Gleichung 5) zu einem System von n unabhängiger Einzelfreiheitsgrad-Differentialgleichungen zweiter Ordnung:
für i =1, ..., n (Gleichung 9)
(Gleichung 9) wird mit Schritt-für-Schritt-Integrationsmethoden wie Wilson-Theta und Newmark gelöst.
Die Integration wird in der Zeitdomäne ausgeführt, wo die Ergebnisse des letzten Schritts für eine Vorhersage des nächsten Schritts herangezogen werden.
Der Verschiebungsvektor (u) des Systems wird von (Gleichung 4) abgeleitet.