La función de densidad de energía de deformación unitaria de Mooney-Rivlin se expresa como:
| Constantes de material de Mooney-Rivlin |
Ecuación de densidad de energía |
| Formulación de dos constantes |
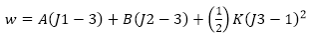 |
| Formulación de cinco constantes |
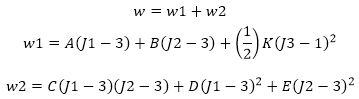 |
| Formulación de seis constantes |
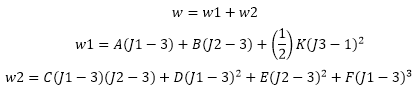 |
- JI, J2 y J3 son las constantes reducidas del tensor de deformación derecho Cauchy-Green y pueden expresarse en términos de cocientes de estiramiento principales
- A, B, C, D, E y F son las constantes materiales primera, segunda, tercera, cuarta, quinta y sexta del modelo de material Mooney-Rivlin. Estas constantes se introducen en el cuadro de diálogo Propiedades de material.
 , = Coeficiente de Poisson
, = Coeficiente de Poisson
A medida que el material se acerca a la incompresibilidad, debe tenerse en cuenta que la tercera constante III se acerca a la unidad mientras que K se acerca al infinito. Por lo tanto, en los valores del coeficiente de Poisson cercanos a 0,5, el último término en W1 permanece dentro de los límites y es posible obtener una solución.
El modelo de material de Mooney-Rivlin puede utilizarse con elementos sólidos y vaciados gruesos.
Las constantes de Mooney-Rivlin se calculan automáticamente cuando la opción Usar datos de curva para computar constantes del material en el cuadro de diálogo Material está seleccionada. Estas constantes se guardan en un archivo de texto con la extensión .log en la carpeta de resultados del estudio activo.