Cuadro de diálogo Material - Pestaña Curvas SN de fatiga

Utilice la pestaña Curvas SN de fatiga para definir las curvas SN de un estudio de fatiga. Las curvas SN solamente se utilizan en estudios de fatiga.

Origen

Para ver este cuadro de diálogo:

Abra una pieza, haga clic con el botón derecho del ratón en Material en el gestor de diseño del FeatureManager y seleccione Editar material.

La pestaña Curvas SN de fatiga solo se encuentra disponible cuando SOLIDWORKS Simulation se encuentra agregado como complemento.

Algunos materiales de la biblioteca de materiales de SOLIDWORKS tienen curvas de fatiga SN previamente definidas. Estos materiales se identifican mediante un sufijo (SN) asociado al final de cada nombre de la lista de materiales de la biblioteca de materiales. La referencia de las curvas de Tensión-Deformación es el Atlas of Fatigue Curves, ASM International.

Establece el esquema de interpolación y el origen de los datos.
Interpolar Establece el esquema para interpolar tensiones alternas contra el número de ciclos de la curva SN.
  • Log-log.

    Interpolación logarítmica (base 10) para el número de ciclos y la tensión alterna. Se recomienda utilizar esta opción para curvas SN con pocos puntos de datos dispersados en ambos ejes, a menos que la curva se ajuste mejor a otro esquema de interpolación.

  • Semi-log. Interpolación lineal para tensión y logarítmica para número de ciclos. Se recomienda utilizar esta opción para curvas SN con un intervalo de tensión relativamente pequeño comparado con la variación en el número de ciclos, a menos que la curva se ajuste mejor a otro esquema de interpolación.
  • Lineal. Interpolación lineal tanto para la tensión como para el número de ciclos. Se recomienda utilizar esta opción para curvas SN con muchos puntos de datos, a menos que la curva se ajuste mejor a otro esquema de interpolación.

    Ejemplo de esquemas de interpolación SN

    En algunos casos, la curva SN está disponible bajo la forma de una ecuación obtenida mediante el ajuste de datos experimentales. En tales casos, si la ecuación coincide con uno de los esquemas de interpolación, se podrían definir sólo los extremos de la curva como puntos de datos y usar el esquema de interpolación adecuado.
Definir Definir los datos de la curva manualmente. Seleccione un máximo de 10 curvas en el menú.
Derivar de módulo elástico de material. Derive la curva SN automáticamente basándose en las curvas SN de ASME y en los módulos de elasticidad del material de referencia y del material activo. El origen SN aparece en el área Vista preliminar.
  • Con base en curvas de acero austenítico ASME
  • Con base en curvas de acero al carbono ASME

La curva SN se obtiene dividiendo cada valor de tensión de la curva SN de referencia por el módulo de elasticidad del material de referencia ASME y multiplicándolo por el módulo de elasticidad del material actual. Los números de ciclos asociados se mantienen sin cambios.

Definir la ecuación de fatiga S-N (para análisis de fatiga de vibración aleatorio) Disponible para los estudios de fatiga que estén basados en los resultados de estudios de vibración aleatoria dinámica.

Datos de tabla

Enumera los datos de la curva. Solo está disponible cuando se selecciona Definir en el cuadro Origen.
Razón de tensiones (R) Disponible solo cuando Personalizado está seleccionado en Seleccionar el origen del material.
Unidades Unidades de tensión alterna.
Si está ingresando los valores asegúrese de seleccionar las unidades que va a desear usar antes de escribir los valores.
Tabla de datos de curva Si está definiendo la curva manualmente, ingrese pares de número de ciclos y valores de tensión alterna. Si la curva se define basándose en una curva de referencia SN de ASME, la curva en escala se encuentra en una lista.
Puede utilizar copiar y pegar para completar la tabla.
File Importa los datos de la curva desde un archivo. Disponible solo cuando Personalizado está seleccionado en Seleccionar el origen del material.
Ver Muestra un gráfico de los datos actuales de la tabla.
Eliminar Elimina la fila de datos seleccionada. Disponible solo cuando Personalizado está seleccionado en Seleccionar el origen del material.
Para aplicar la misma curva SN a sólidos con distintos materiales, en el gestor de estudio de fatiga, haga clic con el botón derecho en Piezas y seleccione Aplicar datos de fatiga a todos los sólidos.

Ecuación de curva S-N (Ecuación de Basquin)

Disponible para los estudios de fatiga que estén basados en los resultados de estudios de vibración aleatoria dinámica lineal.

Constantes de Basquin estimadas para la curva S-N Seleccione esta opción para dejar que el programa calcule las constantes de la ecuación de Basquin en función de los puntos de datos dados de la curva S-N.

Para obtener una fatiga de ciclo alta (número de ciclos N > 104), una curva S-N se puede aproximar por una línea recta cuando se traza en una escala Log-Log. La ecuación de Basquin es una relación de ley de potencia entre los ciclos de tensión (S) en el eje Y y el número de ciclos hasta fallo (N) en el eje X.

La Ecuación de Basquin solo es válida hasta el límite de resistencia o límite de fatiga.
El límite de resistencia es la tensión alterna mayor que no tiene como resultado un fallo por fatiga. En otras palabras, si la tensión alterna es igual o menor que el límite de resistencia, la cantidad de ciclos de tensión que causan fallo se hace muy grande (prácticamente infinita). El límite de resistencia se define generalmente para las tensiones alternas con media en cero. El límite de resistencia también se denomina límite de fatiga. Algunos metales no tienen un límite de resistencia cuantificable.
El programa tiene en cuenta los valores de intervalo de tensión Sr para la ecuación Basquin. Multiplica por 2 los valores de tensión alterna (Sa) de la curva S-N para tener en cuenta una carga completamente invertida (SR = 2*Sa).
La ecuación de Basquin de la curva de fatiga S-N viene dada por:
  • N = B / (Sr) m , o
  • log (Sr) = B - m log (N)
Al seleccionar esta opción, las opciones Constante específica de la curva (B): y Pendiente de la curva S-N (m): están inactivas. El software calcula las constantes B y m colocando una línea recta a través de puntos de datos S-N utilizando la técnica de empalme de línea con el mínimo de cuadrados. Estas constantes son los parámetros de material determinados por los experimentos de pruebas de fatiga en diferentes niveles de tensión.
Unidades Establece las unidades para el intervalo de tensión Sr.
Tenga en cuenta el punto de corte de la curva S-N en la fila Establece el punto de corte de la curva S-N que se tiene en cuenta para el cálculo de las constantes de Basquin. Si introduce 0 o 1, todos los puntos de datos de la curva S-N se tienen en cuenta para el empalme de una línea recta utilizando el método de empalme con el mínimo de cuadrados.
Por ejemplo, si introduce 4, el conjunto de datos del primer conjunto de cuatro filas de la curva S-N se tiene en cuenta para el empalme de una línea recta y el cálculo de las contantes de Basquin B y m. Se recomienda utilizar como punto de corte el límite de resistencia de fatiga. La curva S-N se considera una línea horizontal después del punto de corte.
Constante específica de la curva (B) Introduzca el valor (debe ser un número real positivo) para la constante B específica de S-N. Este es el valor del intervalo de tensión Sr en un ciclo.
Pendiente de la curva S-N (m) Introduzca el valor (debe ser un entero positivo) para la pendiente de la curva S-N m. Cuando se conocen dos puntos de datos (N1, S1) y (N2, S2), la pendiente de la curva S-N m está dada por: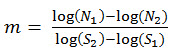
Origen Introduzca información sobre el origen de los datos de S-N.
Ver Seleccione esta opción para ver un gráfico de la curva S-N.
Save Guarda datos de la curva S-N en un formato de archivo *.dat o *.csv (delimitado por comas).