基于响应应力功率波谱密度 (PSD) 函数的统计属性在频率域内估算在随机振动环境中工作的零部件的疲劳损坏评估。
当结构或机械零部件受制于随机载荷形式时,例如风力荷载下的风力涡轮机、波浪荷载下的海洋结构或在不同路面上运行的汽车发动机,在频率域内执行疲劳寿命评估。
术语振动疲劳(或基于频率的疲劳)是指对疲劳寿命的评估,其中荷载和响应(应力和应变历史)是随机流程,且因此使用统计测量(例如,功率波谱密度(PSD 函数))对其进行最佳描述。
可通过 PSD 函数的惯量获得响应应力 PSD 的统计特性。
| PSD 的统计特性 |
方程 |
| 频率为 f(以 Hz 为单位)时应力 PSD S(f) 的第 n 个谱矩。 |
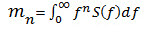 (方程式 1) (方程式 1)
|
| 连续平稳高斯过程 σ 的均方根值。 |
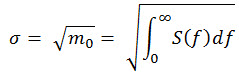 (方程式 2) (方程式 2)
|
| 以典型值 1 秒为采样周期时,上升过零 E[0] 的平均数。 |
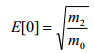 (方程式 3) (方程式 3)
|
| 以典型值 1 秒为采样周期时,峰值 E[p] 平均数。 |
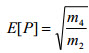 (方程式 4) (方程式 4)
|
| 不规则因数 γ 在 0 和 1 之间变化。当应力接近窄带过程(正弦波 γ =1)时,它接近 1。当应力信号接近白噪声过程时,它收敛到 0.745。 |
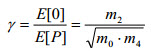 (方程式 5) (方程式 5)
或
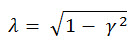 (方程式 6) (方程式 6)
|
材料疲劳属性通常从 S-N 曲线获取,S-N 曲线定义应力方位之间的关系,S(这是从最大受拉周期性应力到最小受压周期性应力的应力变化)与平均失效周期 N。
对于大多数高循环疲劳问题(N >= 104),S-N 曲线可通过以下简化形式表示:
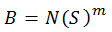 (方程式 7)
(方程式 7)
其中 B 和 m 是随荷载和环境条件变化而变化的材料属性,并且由疲劳测试实验所决定。
随机荷载疲劳导致的累积损坏 E[AD] 基于密纳法则,并表示为:
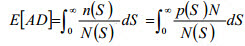 (方程式 8)
(方程式 8)
其中 n(S) 是应力范围级别 S 处应用的循环数,p(S) 是应力范围的概率密度函数。 对上面方程式中的简化 S-N 曲线进行等量代换,可通过以下方程式从随机应力响应获得疲劳损坏的一般方程:
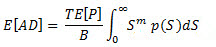 (方程式 9),其中 T 是随机载荷时间长度(以秒为单位)。
(方程式 9),其中 T 是随机载荷时间长度(以秒为单位)。
基于方程式 9 估算疲劳损坏的方法有三种: 斯坦伯格三频带方法、窄带方法和 Wirshing 方法。 每种方法对概率密度函数 p(S) 使用不同的定义。
窄带方法
在窄带方法中,窄带信号的峰值概率密度函数趋向于瑞利分布(Bendat J.S.,随机响应的概率函数。 NASA 接触报告 NASA-5-4590,1964)。
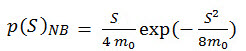 (方程式 10)
(方程式 10)
在(方程式 9)中代换(方程式 10),并将结果整合到以下疲劳损坏估算表达式中。
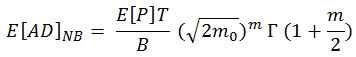 (方程式 11),其中 Γ(.) 是伽玛函数。
(方程式 11),其中 Γ(.) 是伽玛函数。
Wirsching 方法
Wirsching 方法(Wirshing、P.H.、Paez、T.L. 和 Ortiz K.、随机振动,John Wiley & Sons Inc.,纽约,1995)使用经验修正系数修改窄带方法,以考虑宽带过程。
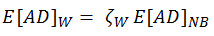 (方程式 12)
(方程式 12)
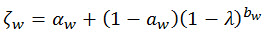 、(方程式 13)
、(方程式 13)
ζw 是从 Monte Carlo 模拟得出的经验系数,包括各种频谱密度函数。
αw 和 bw 是以下方程式给出的最佳拟合参数:
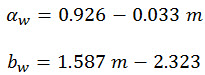 (方程式 14)
(方程式 14)
斯坦伯格三频带方法
斯坦伯格方法的假设是:随机应力响应的概率密度函数遵循高斯分布,因此应力响应幅度的预期值受特定概率水平的约束:
- 68.27% 的机会,应力周期的幅度不超过应力响应信号均方根的 2 倍范围。
- 27.1% 的机会,应力周期的幅度不超过应力响应信号均方根的 4 倍范围。
- 4.3%,应力周期不超过应力响应信号均方根的 6 倍范围。
不存在超过 6 倍均方根范围的应力周期。
预期的疲劳损坏由以下方程式给出:
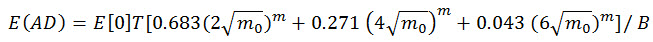 (方程式 15)
(方程式 15)
在模拟中,应力 PSD 函数是疲劳算例所基于的动态-随机振动算例得到的结果。 采用这三种方法计算疲劳导致的预期损坏时,都会考虑 vonMises 应力分量。