Odhad chyby napětí je založen na principu spojitosti pole napětí. Obrázek napětí ERR: Chyba normy energie poskytuje odhad nespojitosti pole napětí od jednoho prvku k jinému.
Uzlová napětí každého prvku jsou průměrována k vyhlazení nespojitosti v napětích prvků napříč hranicemi prvků. Například pro N prvků, které sdílejí stejný uzel, software Simulation sečte hodnoty napětí ze všech prvků a vydělí hodnotou N k výpočtu průměrných hodnot napětí na příslušném uzlu. Funkce tvaru posunutí (lineární nebo polynom vyššího řádu) se používají k interpolaci nového pole napětí.
Odhad chyby napětí v každém prvku je definován jako rozdíl mezi napětím prvku a průměrem uzlových napětí opravených pomocí funkcí tvaru. Tato chyba napětí se používá k výpočtu chyby normy energie pro jednotlivé prvky.
Vyberte složku napětí ERR: Chyba normy energie k vykreslení chyby normy energie pro jednotlivé prvky. Obrázek ERR: Chyba normy energie je dostupný pouze pro statické a pádové zkoušky.
V tabulce jsou shrnuty definice a vzorce pro odhady chyby napětí.
| Definice |
Vzorce |
| Vektor chyby napětí |

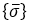 : průměrný vektor napětí na uzlu. Pokud existuje N prvků, které sdílejí stejný uzel, hodnoty napětí ze všech N prvků se sečtou a vydělí hodnotou N. : průměrný vektor napětí na uzlu. Pokud existuje N prvků, které sdílejí stejný uzel, hodnoty napětí ze všech N prvků se sečtou a vydělí hodnotou N.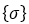 : vektor napětí prvku v uzlu (zprůměrovaný mezi Gaussovy body v každém prvku). : vektor napětí prvku v uzlu (zprůměrovaný mezi Gaussovy body v každém prvku).
|
| Odhad chyby napětí prvku i na základě normy energie |
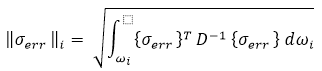
- D: matice tuhosti materiálu nebo základní matice
- w: objem prvku
|
| Odhad globální chyby napětí (celková chyba energie) |
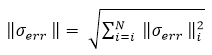
|
| Odhad procentuální chyby prvku (ERR: Chyba normy energie) |
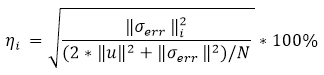
|
| Celková deformační energie |
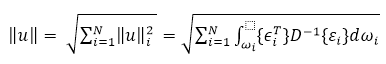
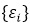 : vektor základní deformace : vektor základní deformace
|
| Průměrná procentní chyba (APE) |
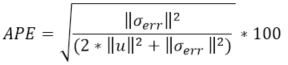 |
- Ve výsledném souboru *.out je uvedena Celková deformační energie. (TSE), Celková chyba energie (TEE) a Průměrná procentní chyba (APE).
- Pokud je síť dostatečně jemná, aby dva sousední prvky měly dokonale souvislé obrysy napětí, chyba napětí na každém uzlu bude nulová. Chcete-li chybu napětí omezit, zjemněte síť v místech s vysokou hodnotou chyby normy energie.
Reference
- A Simple Error Estimator and Adaptive Procedure for Practical Engineering Analysis od autorů O. C. Zienkiewicz a J. Z. Zhu, International Journal for Numerical Methods in Engineering, vol. 24, 337-357 (1987)
- An error analysis and mesh adaptation method for shape design of structural components, od autorů K.-H. Chang a K. Choi (1991), Computers, and Structures Vol. 44. No. 6. str. 1275-1289, 1992 Pergamon Press Ltd.