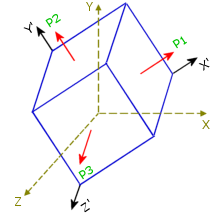
The state of stresses at a point is completely defined by normal and shear stress components in reference to an orthogonal coordinate system XYZ. In general, the values of the stress components change if the coordinate system is rotated.
At a certain orientation (X’Y’Z’), all shear stresses vanish and the
state of stresses is completely defined by 3 normal stress components.
These 3 normal stress components are referred to as principal stresses and
the corresponding reference axes (X’Y’Z’) are referred to as principal axes.
 |
 |
| Figure 1 |
Figure 2 |
At certain orientation of the material element shown in Figure 1, the
shear stress components vanish, and stresses reduce to pure normal stresses as shown in
Figure 2.
You can plot all 3 components at once. The principal stresses at a node
or element center are represented by an ellipsoid. The 3 radii of the ellipsoid
represent the magnitudes of the 3 principal stresses. The direction of the stress
(tension/compression) is represented by arrows. The color code is based on the von Mises
stress values, a scalar quantity.
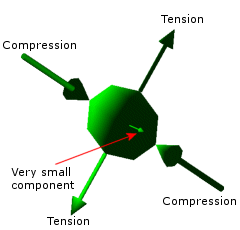
If the three principal stresses have the same magnitude, the ellipsoid
becomes a sphere (Figure 3). If one of the principal stresses is zero, the ellipsoid
becomes a planar ellipse (Figure 4). In the case of simple uniaxial stress, the
ellipsoid becomes a line.
 |
 |
| Figure 3. Three equal principal
stresses in tension. The ellipsoid becomes a sphere. |
Figure 4. One of the principal
stresses is very small. |
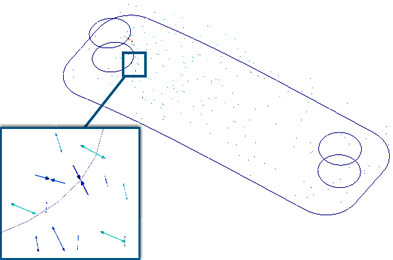
The Principal stress vector shows the magnitude and direction of the
stresses acting on an object. They are represented with double-headed arrows.
 |
Arrows pointing away from each other signifies
tensile principal stress. |
 |
Arrows pointing toward each other signifies
compressive principal stress. |