梁またはトラス、ジョイント条件、および選択された梁の断面特性を定義します。梁では、端部ジョイントへの力とモーメントの伝達を制御します。これは、端部ジョイントにおける力とモーメント成分をゼロに指定できます。拘束は、ジョイントに適用され、それ故、ジョイントに継ぎ合うすべての梁に適用されることに注意してください。
ジョイント終了条件によって、梁と、共通ジョイントに接続する他の梁の間で力とモーメントを伝達できるかどうかが決まります。ジョイントに対する拘束では、アクティブなジョイント条件に関連付けられている自由度の制限のみを適用できます。たとえば、梁の端点をヒンジ(Hinge)として定義し、関連付けられているジョイントに固定(Fixed)拘束を適用しても、指定した梁の端点は、固定(Fixed)拘束に関係なく、自由に回転できます。逆に、梁の端点を剛体(Rigid)として定義し、関連付けられているジョイントに固定(Immovable)拘束を適用した場合、梁の端点は回転できますが、そのジョイントに剛体(Rigid)端を持つ接続梁にモーメントが伝達されます。
Simulation スタディ ツリーで梁定義を右クリックし、定義編集をクリックします。
タイプ(Type)
選択した鋼材レイアウトに要素のタイプを設定します。
|
梁
|
梁要素は、軸、曲げ、ねじり荷重に抵抗します。 |
|
トラス
|
トラス要素は、軸スプリングと同様に軸荷重にのみ抵抗できます。 |
|
梁方向を表示
|
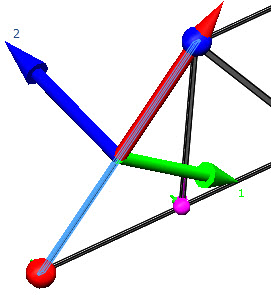
グラフィックス領域における梁方向の表示/非表示を切り替えます。選択した梁で、赤矢印が正の軸方向を表し、緑矢印が方向 1 の正の方向を表し、また青矢印が方向 2 の正の方向を表しています。
|
梁力と梁応力は、梁のローカル座標系に関してリストされます。 軸方向に圧縮荷重を受ける梁やトラスは、軸方向の梁応力値が負の値になり、軸方向に引張り荷重を受ける梁は、軸方向の梁応力値が正の値になります。
端面1結合
梁の端面 1  の力とモーメントを設定します。梁のみで使用されます。
の力とモーメントを設定します。梁のみで使用されます。
梁の端面 1

と端面 2

はグラフィックス領域で異なる色でハイライトされます。
|
剛体
|
この端点では、力、またはモーメントは解放されません。 拘束が関連するジョイントに適用される場合、拘束状態は力とモーメントの伝達を完全に定義します。 拘束が適用されない場合、関連するジョイントで、連続性が想定されます。 力またはモーメント成分をこの端点で解放する理由がないなら、このオプションを使用します。 |
|
ヒンジ
|
端点は自由に回転し、ジョイントへモーメントを伝達しません。ジョイントを中間ヒンジとして定義するには、共通ジョイントで接触するすべての梁の端点にこの条件を適用します。 |
|
スライド
|
端点は自由に伝達し、ジョイントへ力を伝達しません。 |
|
マニュアル
|
それぞれの力とモーメント成分で、手動でゼロにされたか知らせるかを指定します。
|
ヒンジ - 第 1 方向(Hinge- 1st direction)
|
断面の第1方向についてのモーメントを0に設定するときにこのオプションを選択します。端点はこの方向に回転できます。
|
|
ヒンジ - 第 2 方向(Hinge- 2nd direction)
|
断面の第2方向についてのモーメントが0であることが分かっている場合にこのオプションを選択します。端点はこの方向に回転できます。
|
|
ヒンジ - 梁に平行
|
梁の軸方向についてのモーメントが0であることが分かっている場合にこのオプションを選択します。端点はこの方向に回転できます。
|
|
スライド - 第1方向(T)
|
断面の第1方向についての力が0であることが分かっている場合にこのオプションを選択します。端点はこの方向に沿って移動できます。
|
|
スライド - 第2方向(D)
|
断面の第2方向についての力が0であることが分かっている場合にこのオプションを選択します。端点はこの方向に沿って移動できます。
|
|
スライド - 梁に平行(L)
|
梁の軸方向についての力が0であることが分かっている場合にこのオプションを選択します。端点はこの方向に沿って移動できます。
|
|
端面2結合
梁の  の力とモーメントを設定します。オプションは
の力とモーメントを設定します。オプションは  と同様です。
と同様です。
断面/平面特性
SOLIDWORKS データベースから溶接プロファイルを使用する鋼材レイアウトの場合、Simulation では断面特性が計算されます。テーパー付きの梁の場合、梁ボディをメッシュ分割した後、Simulation によって梁の長さ全体にわたって選択された断面の断面プロパティが計算されます。ユーザー定義の梁プロファイルの場合、ユーザー定義の断面特性を入力します。
梁詳細(Beam Details)ダイアログ ボックスには、梁の断面プロパティが一覧表示されます。 梁ボディを右クリックし、詳細(Details)をクリックします。
|
単位
|
最大ねじりせん断応力のねじり定数と距離の計算のための長さの単位です。
|
|
ねじり定数(Torsional Constant)(K)
|
ねじり剛性定数 (長さの 4 乗) を表示します。ねじり定数は梁の断面の関数です。 ソフトウェアは、ほとんどの梁プロファイルに対してねじり定数を計算します。さまざまな断面のねじり定数の理論については、Formulas for Stress and Strain, Roark and Young, Chapter 9, Table 20 を参照してください。
|
|
最大せん断距離(Distance for Max Shear)(CTOR):
|
断面のせん断中心から断面平面上の最も遠い点までの最大距離(せん断中心を中心とする外接円の半径)。  最大ねじりせん断応力は次から計算されます: τ max = (T / K)* CTOR。ここで、T は適用されたトルクです。
|
|
せん断係数
|
せん断係数は、梁の断面にわたる不均一なせん断応力分布で考慮され、梁のせん断変形の計算で考慮されます。その値は、断面の形状と、梁に割り当てられた材料のポアソン比によって異なります。 Simulation では、 『Isoparametric Elements for Cross-sectional Properties and Stress Analysis of Beams』(Karan S. Surana、International Journal for Numerical Methods in Engineering、Vol 14、475-497、1979 年)で説明されている数値法に基づいて、任意の断面を持つ梁のせん断係数が導き出されます。 断面が長方形のほとんどの梁では、せん断係数が 5/6 です。高さと深さの比が変化し、ポアソン比の値が変化する矩形梁の場合、せん断係数は 5/6 と異なる場合があります。次の表を参照してください。
|
|
全選択
|
変数をデフォルト値にリセットします。
|
次の表に、高さと深さの比およびポアソン比(v)が異なる矩形梁のせん断係数を示します。
参照: Shear correction factors in Timoshenko’s beam theory for arbitrary shaped cross-sections, by F. Gruttmann and W. Wagner, Computational Mechanics, Vol 27, 199-207 (2001)
| 高さと深さの比 |
ポアソン比、v = 0 |
ポアソン比、v = 0.25 |
ポアソン比、v = 0.5 |
| 2 |
0.8333 |
0.8331 |
0.8325 |
| 1 |
0.8333 |
0.8295 |
0.8228 |
| 0.5 |
0.8333 |
0.7961 |
0.7375 |
| 0.25 |
0.8333 |
0.6308 |
0.4404 |