지정한 베어링 하중 방향을 기준으로 비대칭 면이나 모서리를 선택할 경우 추가 하중이 적용됩니다. 추가 하중이 적용된 베어링 하중보다 5% 이상일 때 메시지가 나타납니다.
아래 예에서 선택한 요소가 지정한 베어링 하중 방향을 기준으로 대칭하지 않습니다. 원주를 따라 전달된 하중 P의 수평 성분이 명확히 0으로 합산되지 않습니다.
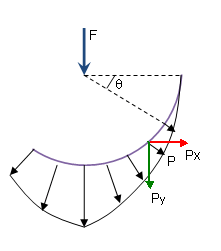
추가의 불균형 하중은 다음 수식으로 계산됩니다.
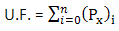
U.F.는 불균형 하중을 나타냅니다.
사인형 하중 분포:
Px = P cosΘ = Fo sinΘ cosΘ
포물선형 하중 분포:
Px = P cosΘ = Fo sin2Θ cosΘ
분균형 하중 비율은 (U.F./F) x 100으로 계산됩니다.
일반적으로, 메시 조절 및 절점 위치는 원주를 따르는 Px의 편차로 인해 불균형 하중의 계산에 영향을 줍니다.