토폴로지에 대한 최소 최대 공식

부품에서 여러 하중 케이스가 작용하는 경우 토폴로지 스터디에서 최소 최대 공식을 사용할 수 있습니다.

여러 하중 케이스에 부품이 종속된 경우 최적화 Goal 강성 대 무게의 최고 비율의 최소 최대 공식은 각 하중 케이스에서 독립적으로 부품 강성을 최대화하거나 컴플라이언스를 최소화하는 해를 구합니다.

예를 들어, 세 개의 독립된 하중 케이스에 종속된 부품의 경우 주어진 진량 감소 구속 조건에 따른 강성 대 무게의 최고 비율에 대한 표준 최적화 공식은 총 컴플라이언스를 최소화하는 해를 구합니다. 컴플라이언스는 구조의 유연성 또는 부드러움을 평가하는 척도이며, 강성과는 상호 보완적입니다. 총 컴플라이언스는 각 하중 케이스에서 독립적으로 계산된 세 개의 컴플라이언스(C1, C2, C3)의 합입니다.

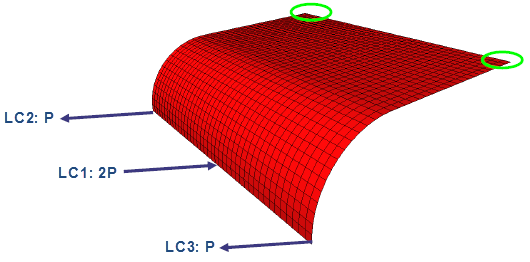
3개의 독립된 하중 케이스: LC1, LC2, LC3이 평판의 쉘 메시 모델에 적용되어 있습니다. 모서리에서 6개 자유도는 고정되어 있습니다.

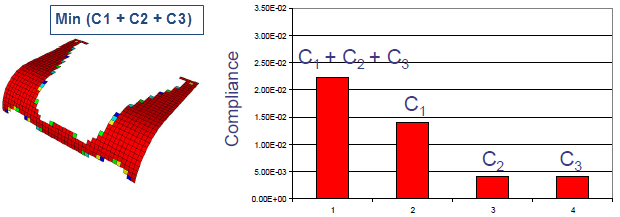표준 공식에서 형상이 최적화되어 있습니다. 40% 질량 감소 구속 조건에 따라 최적화 목표 최소값(C1 + C2 + C3).

최소 최대 최적화 공식은 하중 케이스에서 독립적으로 계산된 최대 컴플라이언스를 최소화하고 각 하중 케이스에서 부품 강성을 최대화하는 해를 구합니다. 부품의 최적화된 형상은 개별적으로 작동할 수 있는 각 하중 케이스에 대해 최대 강성을 가집니다.

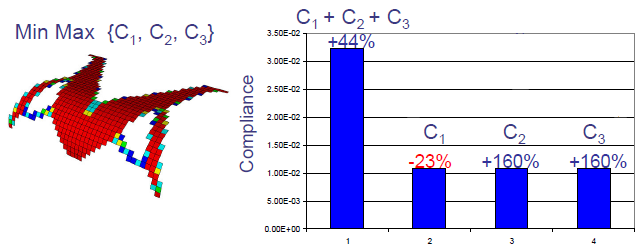최소 최대 공식에서 형상이 최적화되어 있습니다. 40% 질량 감소 구속 조건에 따라 최적화 목표 최소 최대값(C1 + C2 + C3). 최적화된 형상은 독립된 각 하중 케이스에서 강성이 동일합니다.